「6÷2(1+2)」の答えは、「1」なのか「9」なのか? と言う議論があるが、プログラマーが検証してみた。
要件を確認する
プログラマーたるもの、要件/要求仕様を確認するのは常である。
「6÷2(1+2)」の答えは「1」なのか「9」なのか? と、なぜ2通り出てくるのだろうか?
問題は、「2(1+2)」の部分の解釈の違いで次の2通り出てくる。
- 「6÷2(1+2)」の「2(1+2)」を先に計算して、「6÷6=1」とする場合
- 「6÷2(1+2)」は「6÷2×(1+2)」であり括弧内が先なので、「6÷2×3=9」とする場合
どちらが正しいかは結論が出ていないとのことだが、プログラマー的に検証してみる。
視点を変えて見てみる
まず本題に入る前に、「![]() 」を検証してみる。
」を検証してみる。
この式をプログラミング(コーディング)するとき、「x」や「a」は変数のまま変わらい。
べき乗はプログラミング言語により記述が異なるので、ここでは「a^2」とExcelの記述と同じとする。
また、「2a」などの「乗算の演算子×の省略」はできないので、「2×a」であり、また、プログラミング言語では「乗算×」は演算子として「*」を利用するので、「2*a」と記述する。
同じく「除算÷」もプログラミング言語では「/」と記述する。
プログラミング言語でも各演算子には優先順位があり「べき乗^」>「乗算*」=「除算/」>「等号(代入)=」の順となるのも数学と変わらない。 「*」と「/」は同じ優先順位なので、「左から演算する」のも数学と変わらない
以上からプログラミングすると以下のようになる(なってしまう)。
x=6*a^2/2*aこの式がどのようにコンピューターが解釈するのかを分数および約分を使って表すと次になる。
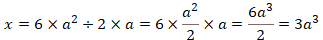
元の式「![]() 」を同様に分数および約分すると次になる。
」を同様に分数および約分すると次になる。
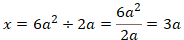
上記のプログラミングの結果は「![]() 」であり、元の式の結果「
」であり、元の式の結果「![]() 」とは違うので、誤ったプログラミングをしていることがわかる。
」とは違うので、誤ったプログラミングをしていることがわかる。
なぜ、このような間違いが出てしまったのだろうか?
プログラミングした、x=6*a^2/2*a では、「2a」の「a」が分子に統合されているのに対し、元の式の「2a」の「a」は分母に行っているという違いがある。
では、どのようにプログラミングすればよいのだろうか?
元の式は結果を変えずに次のように書くことができる。
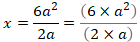
これをプログラミングすると次になる。
x=(6*a^2)/(2*a)このように書けば、元の式の結果「![]() 」と同じになる。
」と同じになる。
最初のプログラミングでは、「2a」は「乗算の演算子×の省略」 したものとして次となった。
x=6*a^2/2*aこの条件は不十分であったことがわかる。
正しいプログラミングでは次となる。
x=(6*a^2)/(2*a)このことから、「2a」は、「括弧と乗算の演算子×を省略」したものが正しいことがわかる。
括弧が付くことから分かるように、「2a」などの『省略された乗算の演算子「×」』は『省略されて無い括弧のつかない演算子「×」や「÷」』より優先順位が高いものであることがわかる。
「6÷2(1+2)」のプログラマーの解釈
本題の「6÷2(1+2)」の「2(1+2)」部分は 「括弧と乗算の演算子×を省略」 したものなので「6÷(2×(1+2))」と書き、結果として次になる。
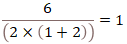
プログラマー的には、このように解釈するのだが、いかがだろうか?
まとめ
「プログラミングするときは、乗算、除算などの優先順位の同じ演算子でもできる限り括弧をつけて分かりやすく書きましょう!」
括弧が多くなると1行が長くなり見づらくなる場合は、改行やインデントするなり、変数を用意して分割しましょう。
今時のプログラミング言語は、最適化で効率よく実行してくれる(効率の良いコード(命令)を生成する)。
また、30年ぐらい前のパソコンのCPUのクロック数が10MHzとか20MHzとかだった頃に比べて、今時のスマホてもは2GHz(=2000MHz,100~200倍)とかで動きます。
さらに、IPC(1クロック当たりの命令実行数)も10倍は言い過ぎかもしれないが、それぐらいになっているはずなので結果として、1000~2000倍とか速いはずなので、少々無駄(冗長)な書き方をしても、問題となるケースはほぼ無いでしょう。(大々的な無駄は問題です)
見やすいプログラミング(コーディング)を心掛けましょう。
2024/1/9追記
最後まで、お読みいただきありがとうございます。
しかし、まだ腑に落ちない方も納得した方も、是非関連項目の 続・「6÷2(1+2)」をプログラマーが検証してみた を参照ください。
なぜ、「括弧と乗算の演算子×を省略」 したものなのかの理由が分かると思います。
ご意見、ご要望、不具合などのご連絡
ご意見、ご要望、不具合などのご連絡は次からお願いします。(2023/05/03追記)
- コメント
本投稿へ下部の コメントを書き込む からご連絡ください。
コメントは承認方式となっており、当方が承認しないと公開表示されません。
公開表示を希望されない方はその旨コメントに記述ください。 - Twitter
ご連絡は @dratech2020 https://twitter.com/dratech2020 の該当ツイートに返信するか、ハッシュタグ「#プログラミングの深淵を求めて」を付けてツイートしてください。 (すぐに気が付かない場合がありますので、ご了承ください)
関連投稿
(2024/01/16追記)
(2023/05/03追記)






コメント
私はプログラマーですが、9だと思います。
基本的にコンピュータは左から計算しますよね。
そうじゃないと辻褄合わないんですが。
ご意見ありがとうございます。
「基本的にコンピュータは左から計算しますよね」と言うより
コーディングするときにどう書きますか?と言うお話です。
例えば
6÷2a をコーディングするとき、
6/2*a とするのが正しいですか?
6/(2*a) とするのが正しいのではないでしょうか?
2aは、”*”のみを省略したものではなくて、”()”と”*”を省略したものではありませんか?
と言うのがこの記事の要点です。
元の式の
6÷2(1+2) をコーディングするときも
6/2*(1+2) とするのが正しいですか?
6/(2*(1+2)) とするのが正しくありませんか?
と言うものです。