コラッツ予想の式の開始時のnと、それから求められるコラッツ数列に着目した考察です。
本件は徹底解説 コラッツ予想のからくりやコラッツ予想をプログラマーが検証してみた の説明では不採用としたものですが、「しくじり先生」的に公開することにしました。
本記事に関連する新しい投稿があります(2023/07/05追記)
目次
はじめに
開始時のnは、偶数と奇数だけでなく、別の仕分けができるのでは無いか? との考えから検討したものです。
開始時のnに着目して考察する
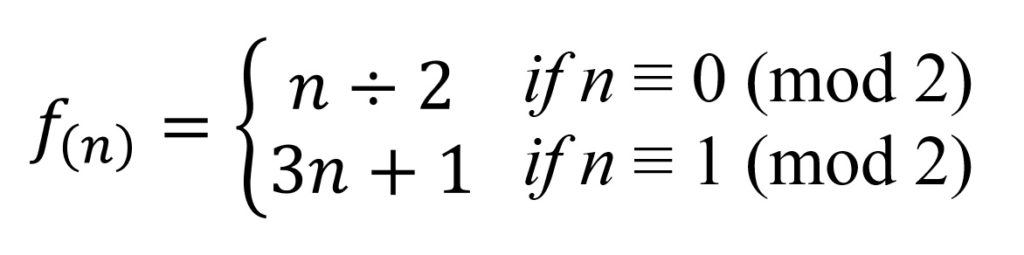
コラッツ予想の式の開始時のnはすべての正の整数を指定できる以上、nが偶数時のf(n)=n/2 のf(n)もまたすべての正の整数となる。
しかし、nが奇数時のf(n)=3n+1 のf(n)はすべての正の整数となることはない。
これらから、開始時のnはあくまでも人工的に与えたものであり、f(n)=n/2 と f(n)=3n+1 とのやり取りでのみで発生する純粋なコラッツ数列と区別できるのではないか? と、考えることができる。
コラッツ数列を眺めて気が付くこと
開始時のnに対して0~31(n=0は正の整数では無いが)の32通りそれぞれで開始したときのコラッツ数列を次の図に示す。(偶数時で開始した時も記述している)
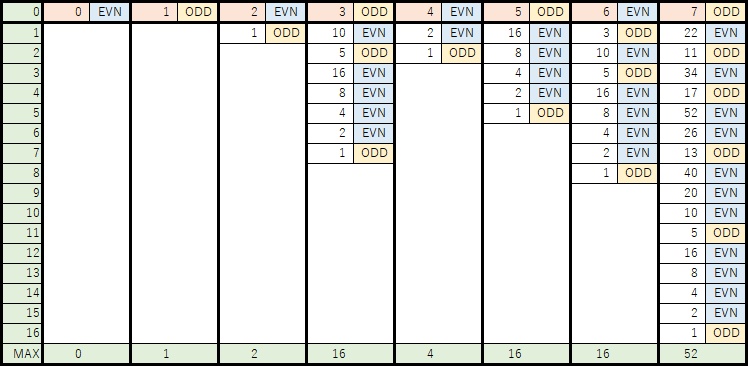
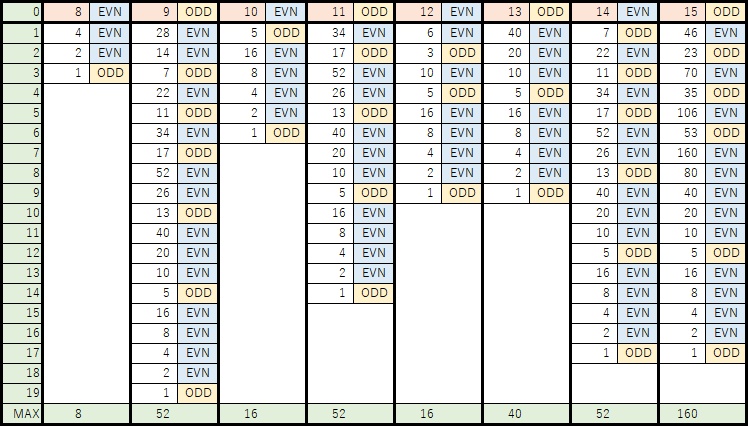
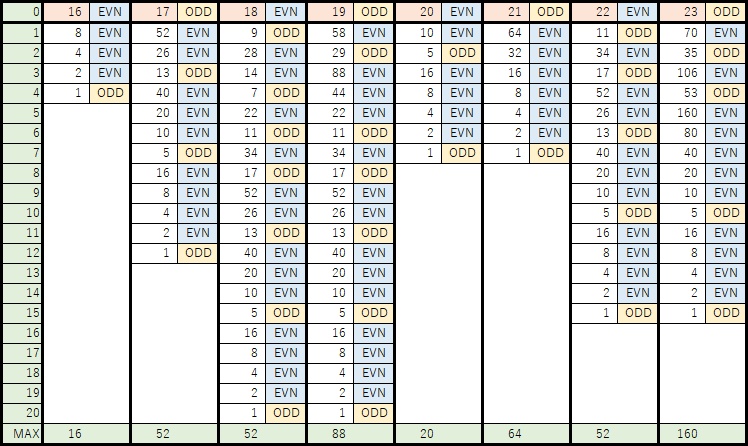

これらの図から次のことが読み取れる。
- 「12」と「13」の数列は、STEP=3より前は別の数列をたどるが、STEP=3以降は同じ数列になる。
その他、「14」と「15」、「18」と「19」、「20」と「21」、「22」と「23」、「24」と「26」、「28」と「29」と「30」なども同じような数列となっている。 - 最大値(MAX)が52のものが、「7」「9」「11」「14」「17」「18」「22」「28」と、32パターン中8パターンと1/4を占める。
その他、最大値が16、88なども多い。 - 「27」の数列は、最初にSTEP=111となることで知られているが、STEP=5で31になるので、それ以降は「31」の数列と同じである(MAX=9232も同じ)。
0~31までの32通りの数列を眺めただけでも、これぐらいのことがすぐに読み取れる。
想像できること
開始時のnはあくまでも人工的に与えたものであるため、f(n)=n/2 と f(n)=3n+1 とのやり取りでのみ発生する純粋なコラッツ数列に至るまでの数値の揺り戻しが発生しているのでは無いか? と、言うことが想像できる。
最後に
私が当時やろうとしていたことは、nは増加して2のべき乗(“1″が立っているビットが1つ)になり、結果として”右にビットシフト”して”1″に到達するであろうこと の検証が目的であり、今回のものはこれとは関係なさそうだとの判断から、これ以上は追及してません。
コラッツ数列を求めるとき、通常nは奇数のみで開始することが多いですが、偶数で開始した数列も見るとわかることが多くなる。
既成概念に捕らわれず、対象を分析することは、非常に重要です。
『我々は同じものを見ている。しかし、角度、つまり立ち位置や立場などが違えば、違って見えるはずだ。』ということで、目的を達成するための手段を得るうえで、既成概念に捕らわれず、対象を分析することはプログラミングでも大いに役立ちます。
この例が何かの役に立てば幸いです。
ご意見、ご要望、不具合などのご連絡
ご意見、ご要望、不具合などのご連絡は次からお願いします。
- コメント
本投稿へ下部の コメントを書き込む からご連絡ください。
コメントは承認方式となっており、当方が承認しないと公開表示されません。
公開表示を希望されない方はその旨コメントに記述ください。 - Twitter
ご連絡は @dratech2020 https://twitter.com/dratech2020 の該当ツイートに返信するか、ハッシュタグ「#コラッツ予想のからくり #プログラミングの深淵を求めて」を付けてツイートしてください。 (すぐに気が付かない場合がありますので、ご了承ください)
関連投稿
ツール:Excel版
ツール:ブラウザ(BigInt)版
徹底解説 コラッツ予想のからくり
これらの投稿は下記の「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。
#1 特徴&論理編
#2 からくり編
#3 結論&証明編
コラッツ予想のからくりのまとめ
コラッツ予想をプログラマーが検証してみた
#1 要件を確認する
#2 Excelで作ってみた
#3 さらに角度を変えて検証したら・・・!!!
#4 最後に
コラッツ予想のからくり Extra Stage
#1 「1→4→2→1→…のループ」がすべてを飲み込む!?
#2 コラッツ数列は偶数奇数以外に仕分けできる!? (本記事)





コメント