徹底解説 コラッツ予想のからくり #1 特徴&論理編

プログラミング
2021.11.01
スポンサーリンク
スポンサーリンク

コラッツ予想を証明できたと考えるので、そのからくりをまとめる。
まずは、コラッツ予想の特徴と論理をまとめる。

本記事に関連する新しい投稿があります(2023/07/05追記)

iCollatzの提案 まとめ
コラッツ予想のからくりでは、2進数で見ると直感的に解りやすいことを示した。 しかし、「2進数なんて馴染みがないよ! 10進数で見やすくできないか?」との意見が出るであろうことを想定して作ったのがiCollatz/Infinite Colla...
www.seekabypro.com
2023.06.21

はじめに

コラッツ予想に対して、見る角度を変えた検証の結果(関連投稿参照)、その証明ができたように考えています。
そのからくりを、今までの検証結果から要点のみ抽出し再構築、説明不足だった部分を加筆してまとめます。
もし、これで証明できてなかったとしても、このようなアプローチのやり方があると言うことを示せれば数学の発展に貢献できると考えて公開します。

以下に示す構成を予定しており、すでに公開している検証結果からの再構築であることもあり、順次公開していく予定です。

  • 特徴&論理編(本投稿)
  • からくり編
  • 結論&証明編

これらの内容を元に数学論文を作成中ですが、私の専門ではない慣れないものなので、なかなかうまく進んでいません。
検証記事はすでに公開している内容であり、また、数学論文では言い回しは変わるかもしれませんが、論理そのものは変わらないので本サイトで公開しつつまとめていきます。

本サイトで公開している投稿の内容だけで「証明は十分」だと考えています。
しかし、数学論文には、証明をより強固とするため、未公開の論理を記述します。
その論理は数学論文を提出した後、頃合いを見計らって本サイトでも公開予定です。

関連投稿

コラッツ予想をプログラマーが検証してみた

#1 要件を確認する
#2 Excelで作ってみた
#3 さらに角度を変えて検証したら・・・!!!
#4 最後に

徹底解説 コラッツ予想のからくり

#1 特徴&論理編(本投稿)
#2 からくり編(2021/11/08追記)
#3 結論&証明編(2021/11/15追記)
コラッツ予想のからくりのまとめ (2021/12/20追記)

コラッツ予想とは?

コラッツ予想は、コラッツ問題や3n+1問題などと呼ばれることもある、数学の未解決問題の1つとのことです。

コラッツ予想の式

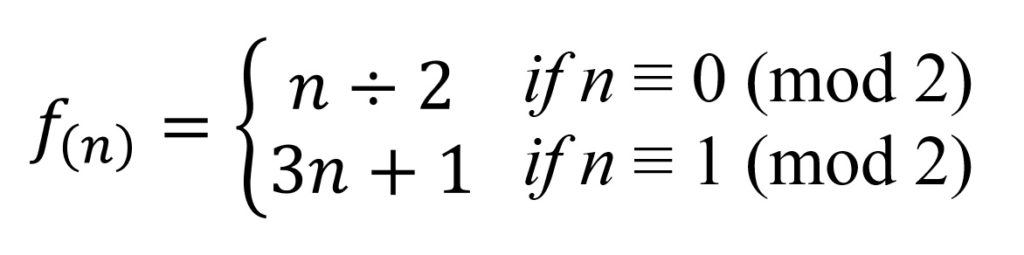
任意の正の整数をnとして入力したとき

  • nが偶数(2で割った余り(mod)が0)の場合は2で割る。その結果を次のnとする。
  • nが奇数(2で割った余り(mod)が1)の場合は3倍して1を足す。その結果を次のnとする。

この計算を繰り返した時、すべての正の整数nで開始しても、最終的に1に到達する(正確には1→4→2→1→…と無限ループになる)と言う予想がある。

3n+1の”3″とn÷2(以下n/2と記述する)の”2″は、”3″の方が大きいので、nは増加するように感じるが、実際に計算を繰り返していくと、nは減少してn=1に到達すると言う矛盾した結果にたどり着く。

執筆時点で多くの数値(270ぐらい?)で確認されているが、すべての正の整数nで開始しても、増加せずに減少して”1″に到達する仕組み(からくり)は長年解明されておらず、予想と言う表現になっている。

まずは、このコラッツ予想の式を見てみると、以下の特徴が抽出できる。

[特徴1]偶数と奇数の2種類の数値を扱うこと
[特徴2]n/2が2進数では”右に1ビットシフト”であること(後述)
[特徴3]到達点の”1″、および、”1→4→2→1→…”の無限ループの各数値が、2のべき乗(1=20, 2=21, 4=22)であること

これらからコラッツ予想の式は“2進数”との親和性が高いことが分かる。

関連投稿の「コラッツ予想をプログラマーが検証してみた」を読むと分かるので書いてしまいますが、[特徴2]と[特徴3]からnは増加して2のべき乗(“1″が立っているビットが1つ)になり、結果として”右にビットシフト”して”1″に到達するであろうことがこの時点で想像できます。

私は、闇雲にコラッツ予想の証明に挑戦したのではなく、この想像が正しいかどうかを多少迷いながら(この部分は未公開ですが機会があれば公開するかも)も、目標に向かって方向を修正しつつ求めたものです。

2進数とは?

2進数に馴染みがない方のために、少しここで説明しておきます。

我々が一般に使う10進数は0～9の10種類の数値を使う。
0から1ずつ足すと、0,1,2,3,4,5,6,7,8,9となるが、9に1を足すと桁上がりして10となるものであり、同様に99に1を足すと桁上がりして100となる。

一方、2進数は0と1の2種類の数値を使う。
同様に1ずつ足すと、0,1となるが、1に1を足すと、桁上がりして10(「ジュウ」とは読まず「イチゼロ」や「イチマル」などと読む)となるものであり、同様に11(「イチイチ」と読む)に1を足すと桁上がりして100(「イチゼロゼロ」や「イチマルマル」などと読む)となる。
10進数で”2″の時は2進数では”10″となり、 10進数で”4″の時は2進数では”100″となる。

2進数の桁のことを”ビット(bit)”とも呼ぶ。
2進数で64桁のことを64bitと呼び、スマートフォンやPCのカタログなどで見たこともあると思う。
2進数はこれらのデジタル機器の根幹の1つとなっています。

2進数の”1″が1つだけ立っているとき、“0”の個数がその数の指数部の2のべき乗と一致する。

指数部2のべき乗10進数2進数
02011
121210
2224100
32381000
4241610000
::::

例えば、2進数で”1000″のとき、”0″は3個なので、指数部が”3″の23=8となる。

10進数より2進数で見る方が良い理由

10進数で、”1,048,576″という数値を見てこれが何かすぐにわかりますか?
これは、スマートフォンやPCなどのコンピューターの世界でよく見る”1M(メガ)”の素の値です。

  1,048,576
= 1M(メガ)
= 1K(キロ) × 1K(キロ)
= 1,024 × 1,024
= 210 × 210
= 220

10進数の”220“は、2進数で”10000 00000000 00000000″(“1″と”0″が20個)と、とても簡単なビットパターン(文字列)の数値となる。
これは一つの例ですが、10進数で見ていてもそれが2のべき乗であることに気が付く人は少ないだろうと思います。

ちなみにこの”1,048,576″を開始時の入力nとしてコラッツ数列を求めると、途中で奇数(ODD)となることなく、”1″に到達します。

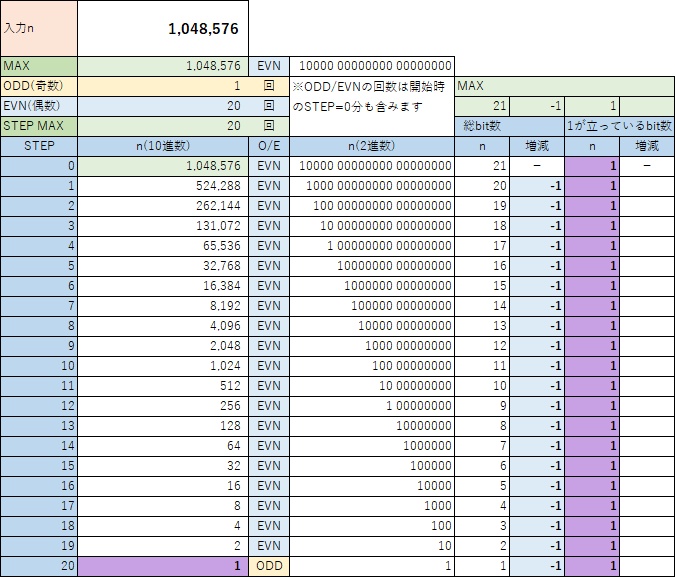
次に、10進数で”1,049,089″を見てどう思いますか?
先ほどの”1,048,576″より大きいと言うことぐらいは分かると思いますがそれ以外はすぐには気が付けません。

  1,049,089
= 1,048,576 + 512 + 1
= 220 + 29 + 20

10進数で見た時”1,049,089″=”1,048,576 + 512 + 1″であることにすぐに気が付くことはできません。

この”1,049,089″の2進数は”10000 00000010 00000001″であり、とても簡単なビットパターンです。
これは2進数では次の足し算になります。

  10000 00000010 00000001
= 10000 00000000 00000000    ←10進数で220 = 1,048,576
 +            10 00000000    ←10進数で29  =       512
 +                      1    ←10進数で20  =         1

コラッツ予想の式が”2進数”と親和性が高い特徴と合わせて、10進数で見るより2進数で見た方が直感的に理解できることを表しています。

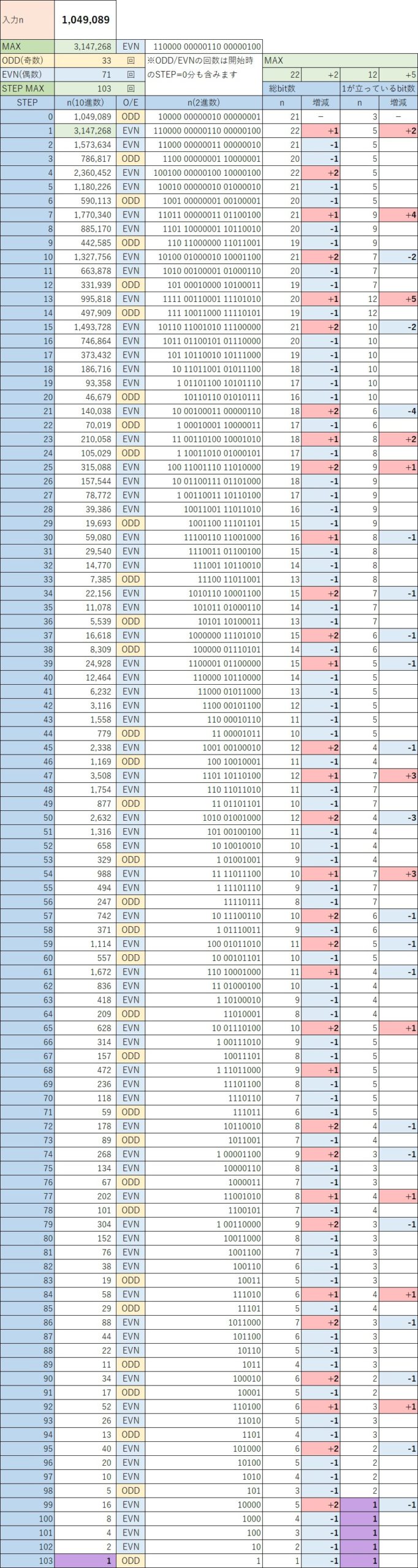
補足に “1,049,089”を開始時の入力nとしてコラッツ数列を求めたものを掲載します。

また、2進数は”0″と”1″の2種類の文字しか使えず、”1″の部分は2のべき乗に対応するので、すべての正の整数は2のべき乗の組み合わせ(足し算)で表せます。
なお、2のべき乗の指数部(上記の例の”20″と”9″と”0″)は、重複することはありません。

29 + 29 = 512 + 512 = 1,024 = 210

29(指数部”9″)と29を足すと210(指数部”10″)となってしまうため、指数部の組み合わせに重複はない(この例では”9″は重複せず”10”になる)。

偶数と奇数の判定方法

nが偶数か奇数か判定するとき、nを2で割った余りを見る必要があるが、10進数では最下位の桁(右端の桁、100の桁)を見て判断できる。

"0","2","4","6","8"が偶数
"1","3","5","7","9"が奇数

10進数で”1,048,576“の最下位の桁は”6“なので偶数。
“1,049,089“の最下位の桁は”9“なので奇数。

2進数でも最下位ビット(最下位の桁、右端の桁、20の桁)を見て判断できる。

"0"が偶数
"1"が奇数

同様に2進数で”10000 00000000 00000000“の最下位ビットは”0“なので偶数。
“10000 00000010 00000001“の最下位ビットは”1“なので奇数。

[論理A]nを2進数で見たとき、最下位ビット(20の桁)が”0″であれば偶数、”1″であれば奇数である

nが偶数時の”n/2″について

例えば10進数で”2,340/10″を計算するとき、結果は最下位の桁の”0″を消して”234″と暗算できる。
これは、最下位の”0″を切り捨てし”234″を右に1桁移動したものである。

10進数の”2″は、2進数では”10″となる。
10進数で書いた”n/2″は、2進数では”n/10″である。

例えば2進数でn=”1001 00100100″(10進数で”2,340″)としたとき、n/10は次のようになる。

  1001 00100100 / 10     ←10進数で 2,340 / 2
=  100 10010010          ←10進数で 1,170

“10進数の2,340/10″の例と同じように、最下位の桁の”0″を消して暗算できる。
これも、最下位の”0″を切り捨てし”100 10010010″を右に1桁移動(シフト)したものである。
このようなものをビット演算では、“右に1ビットシフト”と言う。

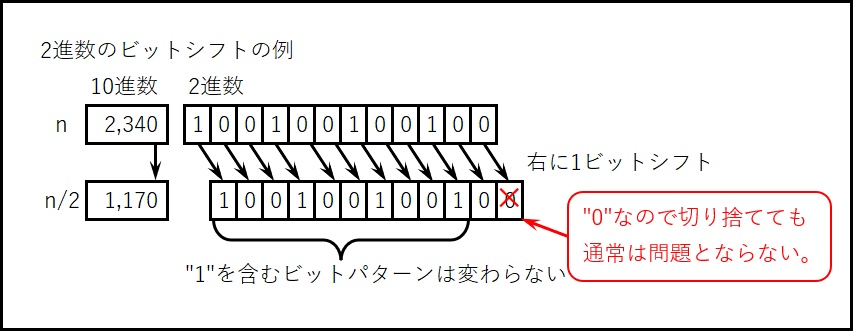
nが偶数の場合、最下位ビットは”0″のため、“右に1ビットシフト”による”0″の切り捨て(アンダーフロー)は通常問題とならない。

また、数値の要素となる”1″を含んだビットパターンは演算の前後で変化しない(2進数のときの文字列パターン:例では”100 1001001″の部分)。

[論理B]”n/2″は2進数では”右に1ビットシフト”であり、数値の要素となる”1″を含んだビットパターンは変わらない

なお、10進数のn/2をビット演算では”右に1ビットシフト”と呼ぶように、n*2を”左に1ビットシフト”と言い、不足した最下位ビット(20の桁)に”0″を埋める。

指数部2のべき乗10進数2進数
02011
121210
2224100
32381000
4241610000
::::

2のべき乗の2進数の”1″が、”*2″(指数部が+1)される毎に”左に1ビットシフト”していることがわかる。

nが奇数時の”3n+1″について

“3n”について

“3n+1”の”3n”は、nのすべての桁を等しく3倍する。
例えば、10進数でn=”3,003″のとき、”3n”は”9,009″となる。
nの”0″の桁は3倍しても”0″なだけで、3倍したことに変わりない。
また、nが奇数である限り、nの3(奇数)倍の結果は必ず奇数となる。

“+1″について

“3n”に、”+1”すると言うことは、上位の桁のグループより下位の桁のグループの方が速く増加する。

 9,009 + 1
=9,010

“+1″しても上位の桁のグループは”9“のままで、下位の桁のグループは”9“→”10“となり、速く増加する。
“+1″して上位の桁のグループに影響を及ぼすのは、桁上がりが発生したときのみである。

また、”3n”が必ず奇数となるので、“+1″すると結果は必ず偶数となり、下位の桁のグループには2のべき乗(20=1は奇数なので除く)を含む。

3n+1の結果は必ず偶数となる

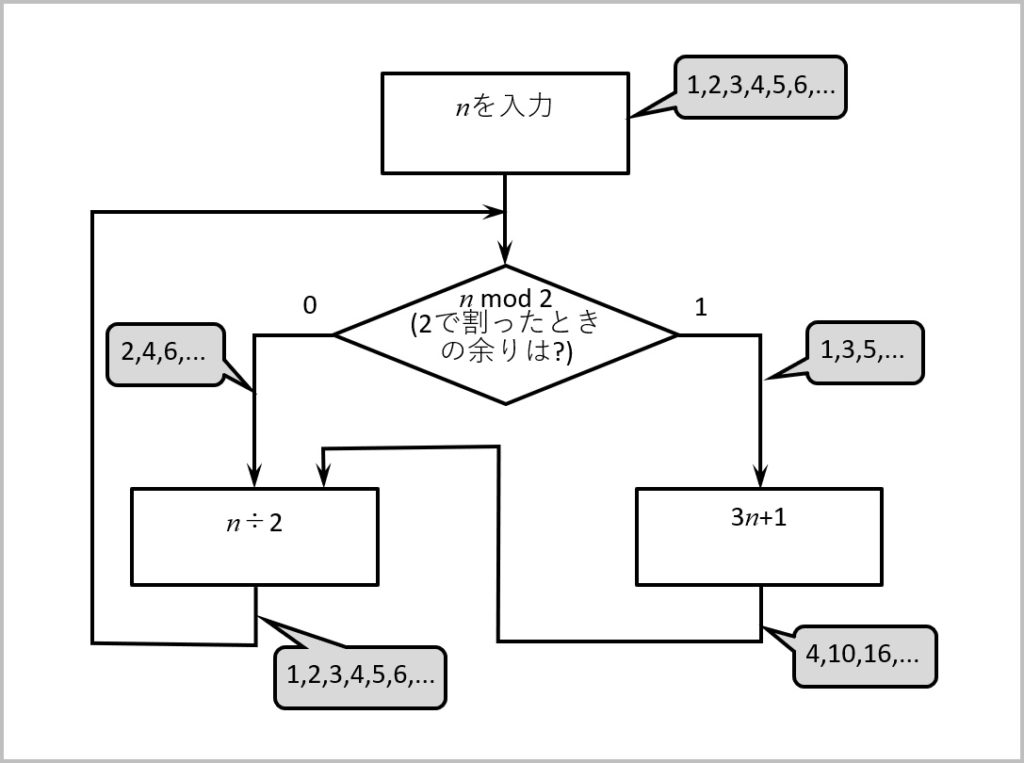
これらは数値の見方を変えただけの2進数でも同じである。

10進数2進数
n3,0031011 10111011
3n9,009100011 00110001
3n+19,010100011 00110010

“3n+1″の2進数”100011 00110010“の下位の”10“が2のべき乗(10進数で21=2)であることがわかる。
下位のグループの増加が速いことは10進数では見やすいが2進数では見にくいので、n=”33″(2進数で”100001″)の例を次に示す。

10進数2進数
n33100001
3n991100011
3n+11001100100

“3n+1″の2進数”1100100“の上位の桁のグループ”11“より、下位の桁のグループ”100“の方が速く増加していることがわかる。
また、下位の”100“が2のべき乗(10進数で22=4)であることがわかる。

[論理C]”3n+1″の結果は必ず偶数となり、下位の桁のグループに2のべき乗を含む
[論理D]”3n+1″の”+1″により、上位の桁のグループより下位の桁のグループの方が速く増加する

無限ループについて

コラッツ予想では”1″に到達することをゴールとしているケースが多いが、その後、 “1→4→2→1→…”の無限ループになることが分かっている。

これは、nが”1″に到達したとしても、“3n+1″を含めて無限に繰り返すことを表している。

“3n+1″を無限に繰り返すと言うことは、[論理D]からいずれ下位の桁のグループが上位の桁のグループを侵食し、また[論理C]からnそのものが2のべき乗(“1″が立っているビットが1つ)に収束することを表している。

ただし、nが偶数時のn/2との兼ね合いで上記をすり抜けるものがあるのでは無いか?と思うかもしれないが、[論理B]からビットパターンが変わらないため、すり抜けることはない(詳細は今後の投稿で説明します。すぐに知りたい方は関連投稿を参照してください)。

[論理E:要証明]”3n+1″を無限に繰り返すと、nそのものが2のべき乗(“1″が立っているビットが1つ)に収束する

今回のまとめ

特徴

コラッツ予想の式から以下の特徴が抽出できる。

[特徴1]偶数と奇数の2種類の数値を扱うこと
[特徴2]n/2が2進数では”右に1ビットシフト”であること
[特徴3]到達点の”1″、および、”1→4→2→1→…”の無限ループの各数値が、2のべき乗(1=20, 2=21, 4=22)であること

これらの特徴からコラッツ予想の式は”2進数”との親和性が高いことが分かる。

論理

[論理A]nを2進数で見たとき、最下位ビット(20の桁)が”0″であれば偶数、”1″であれば奇数である
[論理B]”n/2″は2進数では”右に1ビットシフト”であり、数値の要素となる”1″を含んだビットパターンは変わらない
[論理C]”3n+1″の結果は必ず偶数となり、下位の桁のグループに2のべき乗を含む
[論理D]”3n+1″の”+1″により、上位の桁のグループより下位の桁のグループの方が速く増加する
[論理E:要証明]”3n+1″を無限に繰り返すと、nそのものが2のべき乗(“1″が立っているビットが1つ)に収束する

次回「からくり編」

次回は、上記の論理を当てはめながら、実際の例を用いて「コラッツ予想のからくり」を説明する。

補足

“1,049,089”で開始したときのコラッツ数列

コメント

スポンサーリンク
タイトルとURLをコピーしました