前回までにわかった 特徴と論理とからくり から結論とコラッツ予想の証明の真偽を確認する。
本記事に関連する新しい投稿があります(2023/07/05追記)
目次
特徴&論理&からくり
前々回、前回、特徴と論理とからくりをまとめたのでここに掲載しておく。
特徴
コラッツ予想の式から以下の特徴が抽出できる。
- [特徴1]偶数と奇数の2種類の数値を扱うこと
- [特徴2]n/2が2進数では”右に1ビットシフト”であること
- [特徴3]到達点の”1″、および、”1→4→2→1→…”の無限ループの各数値が、2のべき乗(1=20, 2=21, 4=22)であること
これらの特徴からコラッツ予想の式は”2進数”との親和性が高いことが分かる。
論理
コラッツ予想の式から以下の論理が導き出せる
- [論理A]nを2進数で見たとき、最下位ビット(20の桁)が”0″であれば偶数、”1″であれば奇数である
- [論理B]”n/2″は2進数では”右に1ビットシフト”であり、数値の要素となる”1″を含んだビットパターンは変わらない
- [論理C]”3n+1″の結果は必ず偶数となり、下位の桁のグループに2のべき乗を含む
- [論理D]”3n+1″の”+1″により、上位の桁のグループより下位の桁のグループの方が速く増加する
- [論理E:要証明]”3n+1″を無限に繰り返すと、nそのものが2のべき乗(“1″が立っているビットが1つ)に収束する
からくり
コラッツ数列に、[論理A~E]を当てはめ、次のからくりが得られた。
- [からくり1]nが偶数になる毎に発生する”右に1ビットシフト”により、数値の基準点となる最下位ビット(20の桁)がSTEP:0(開始時)のn の最下位ビットから左にずれる
- [からくり2]数値の基準点が左にずれるため、”+1″する位置も同様にずれる
- [からくり3]10進数で見た時はn=”1″に到達した時点を”STEP数”としているが、2進数で見た時は2のべき乗となったときを到達点と判断でき”STEP数”に違いがある
- [からくり4]後述
[からくり1]と[からくり2]が、コラッツ予想を直感的に理解することを難しくしている理由である。
[からくり3]は命題ではないので追及はしない
からくりの対策
今までは、単にコラッツ予想の式からわったこと、実際の例を用いてわかったことをまとめた。
しかし、からくりの回避には式の変更が必要となる。
コラッツ予想の式
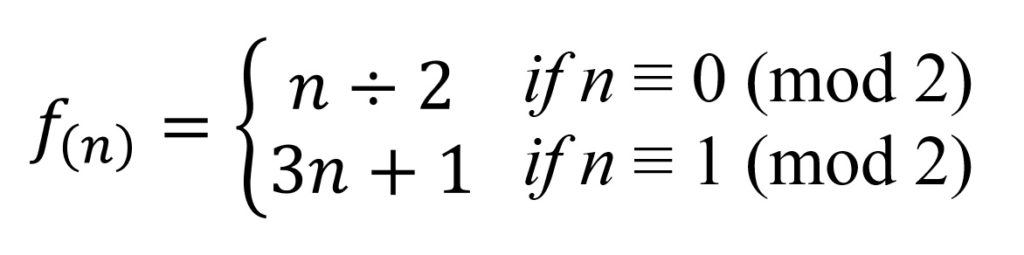
以下、このコラッツ予想の元の式を[元]と表記する。
“右に1ビットシフト”の対策
[からくり1]と[からくり2]の問題は、nの”数値の基準点”が開始時(STEP:0)からずれていくことである。
これをずれないように開始時(STEP:0)のnの数値の基準点=20の桁に固定する。
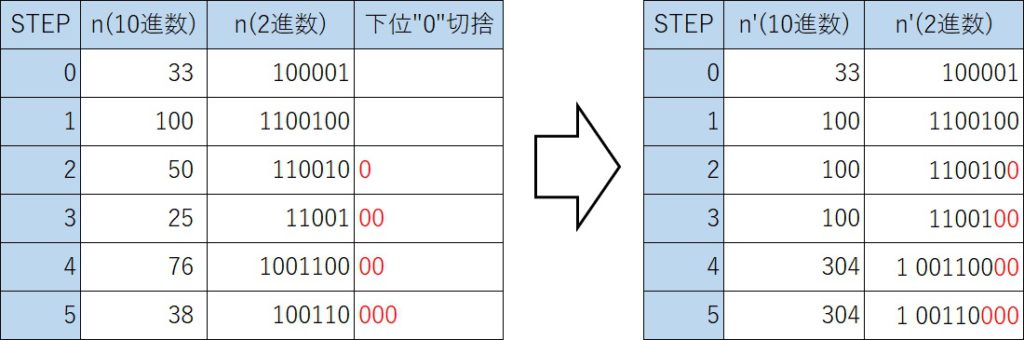
この例のように「n(2進数)」と「下位”0“切捨」の部分の文字列を連結して、 開始時(STEP:0)のnの数値の基準点=20の桁を合わせて表示すればわかりやすくなるが、これだとプログラミングが必須となり不便である。
このため、[元]を変化させることで数式として求めることで、プログラミングすることなく数列が求められるようにする。
“数値の基準点”のずれの原因は”右に1ビットシフト”であり、これはつまり偶数時の”n/2″である。
この“2で割る”の部分を削除するように[元]を変化させていく。
f'(n')=n'偶数時の式をこのように変化させる。
開始時の n’ は n と同じ値だが、繰り返しうちに値が違ってくるので n’ と表記を変える。
また、f も値も違ってくるので f’ と表記する。
“3n”の扱い
[元]の奇数時の”3n+1″の”3n”は、nのすべての桁を3倍し、”0″の桁は3倍しても”0″なだけなので、変更する必要はなく、” 3n’ “となる。
“+1″の対策
[元]の奇数時の”3n+1″の”+1″は、[からくり2]により、開始時(STEP:0)のnの数値の基準点=20の桁から左にずれている。
nが偶数になる毎に左に2進数で1ビットずれるので、2倍にしていく必要があり”+1″の部分を変数に置き換える必要もある。
変数”d”を用いて、初期値を”1″とする。
結果として、奇数時のf'(n’)は次のようになる。
f'(n')=3n'+dまた、n’ が偶数の時に、dを2倍にする必要があるため、次のようにする。
g(d)=2dg(d)は繰り返しの次のSTEPでdとなる。
“d”は初期値が”1″で、n’が偶数となる毎に2倍を繰り返すので、”左に1ビットシフト”を繰り返すのと同じであり、以下の表のように、2進数で見た時、”1″が立っているビットは1つだけである。
| 偶数発生回数 | 2のべき乗 | 10進数 | 2進数 |
| 0 | 20 | 1 | 1 |
| 1 | 21 | 2 | 10 |
| 2 | 22 | 4 | 100 |
| 3 | 23 | 8 | 1000 |
| 4 | 24 | 16 | 10000 |
| : | : | : | : |
なお、変数の”d”は、”デジタル(digital)”、”ドラえもん”、私のニックネーム”どらテク”の”d”である。
“デジタル”なのは、初期値”1″を2倍、2倍…していく2のべき乗を表しているためである。
“ドラえもん”なのは、作中で登場するアイテムに”バイバイン”があり、栗饅頭が一定の時間毎に2倍、2倍…していくエピソードなのだが、知名度の関係から”ドラえもん”とした。
偶数と奇数
数値の基準点がずれないように開始時(STEP:0)のnの数値の基準点=20の桁に固定したため、偶数と奇数の判定もそのままの”20の桁”ではできない。
[元]のnの”20の桁”は、奇数時の”3n+1″の”+1″していた”20の桁”と同じなので、対策後は”d”の”1″の立っているビット位置で判定が可能となる。
判定には、ビット演算子の”ビット毎の論理積”を用い、演算子は”&”とする。
“d”は2のべき乗なので”1″が立っているビットは1つであり、n’ の同じビット位置に”1″があるときが奇数、無いときは偶数となる。
(n' & d) = 0 であれば偶数
(n' & d) > 0 であれば奇数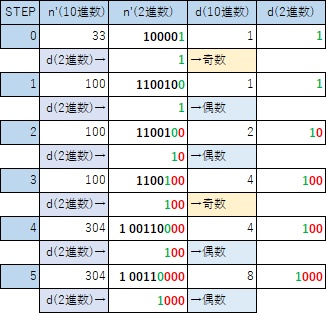
また、数値の基準点を20の桁に固定したため、n’ は[元]のnをd倍したものであり、dは2のべき乗なので2進数ではdの”0″の桁の数だけn’を左にビットシフトしたものである。
n' = nd
→ n = n'/dn’と[元]のn(=n’/d)の関係の例を次に示す。
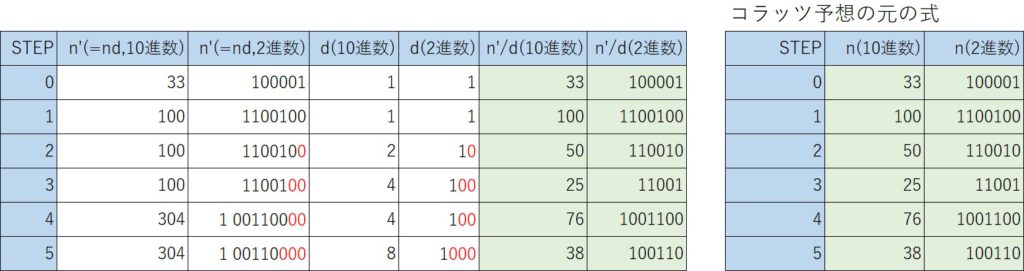
本投稿記事では、偶数と奇数の判定に”ビット毎の論理積”を利用するが、n=n’/d なので、このnの最下位ビットを見て、偶数と奇数の判定を行っても結果は同じとなる。
STEP数について
数値の基準点がずれないように開始時(STEP:0)のnの数値の基準点=20の桁に固定したため、n’ が”1″に到達することは無い(開始時のn’=1のときを除く)。
しかし[からくり3]で示したように n’ が2のべき乗になったときを到達点として、それをSTEP数とする。
コラッツ予想[KAI]の提案
以上、文章で書くと理解しずらいので数式を次に示す。
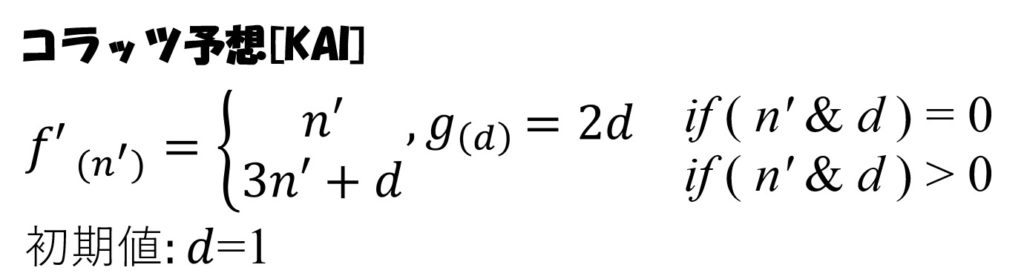
論理’
数式を[KAI]としたことで、論理も変化が発生する。
- [論理A’]n’を2進数で見たとき、”(n’ & d)=0″であれば偶数、”(n’ & d)>0″であれば奇数である
- [論理B’]偶数時のn’に変化はない。代わりにdを”2d”する。これは2進数では”左に1ビットシフト”であり、dの初期値は”1″なので、2のべき乗を保ちつつ増加する。
- [論理C’]”3n’+d”の結果は必ず偶数となり、桁上がりした後、下位の桁のグループに2のべき乗を含む
- [論理D’]”3n’+d”の”+d”により、上位の桁のグループより下位の桁のグループの方が速く増加する
- [論理E’:要証明]”3n’+d”を無限に繰り返すと、n’そのものが2のべき乗(“1″が立っているビットが1つ)に収束する
[KAI]の数列の例
[元]の”33″の例
まずは比較用に[元]の”33″の例を示す。
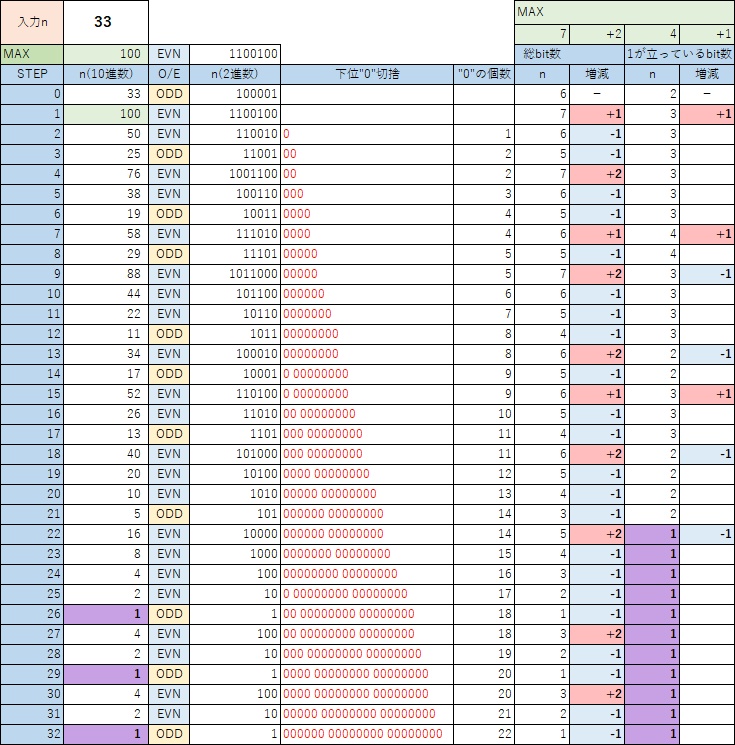
[KAI]の”33″の例
[KAI]の開始時の入力nに”33″を指定したときの数列を次に示す。
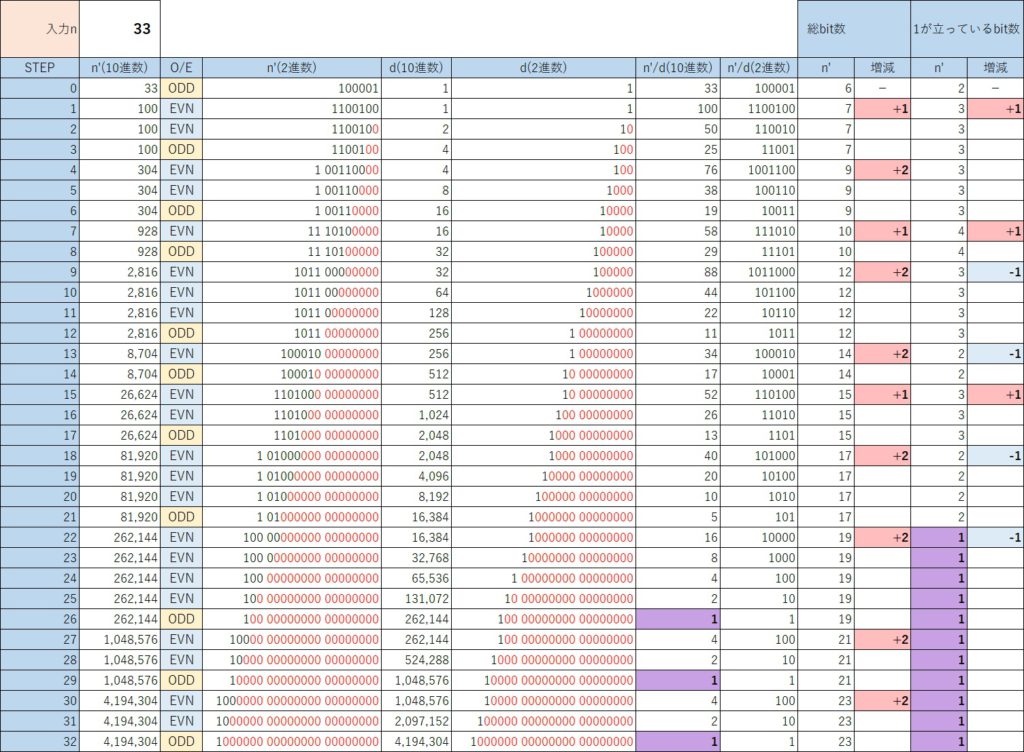
- 「n’/d(10進数)および(2進数)」の数列が[元]の”33″の例の「n(10進数)および(2進数)」と同じになる。
- 「n'(10進数)」と「d(2進数)」の”0“が、[元]の”33″の例では「下位”0″切捨」の部分に対応する。
- 偶数(EVN)時は”d”のみ、奇数(ODD)時は” n’ “のみ増加して、どちらも減少することはない
[論理A’~E’]の適用は、 からくりの対策 の内容であり、前回行った “33”の例に[論理A~E]を適用その2 を”d”の”0“の個数分左にずらしただけなので省略し、要点のみ以下に説明する。
[KAI要点1]
偶数時は”d”のみ、奇数時は” n’ “のみ、それぞれどちらかしか増加しかしないため、どちらかの変数に着目したとき、他方の変数は変化しないので直感的に理解しやすい。
[KAI要点2]
偶数時の”d”は、n’ を2進数で見た時、一番右にある”1″が立ったビットを検索する機能である。
“1”を見つけると奇数時の”3n’+d”を実施するが、見つけた”1″のビット(桁)は”3n’ “しても必ず”1″のままで、”+d”により確実にそのビットに対して桁上がりが発生する。
これにより、”n’ “の”d”以下(図の”0“の部分)のビットに”1″が立っていることは無い。
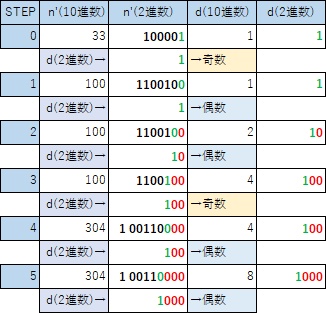
[KAI要点3]
“n’ “は偶数時には[論理B’]により変化はない(ビットパターンも変わるはずはない)。
奇数時の”3n’+d”のみ考えればよい。
[KAI]を繰り返す言うことは、 “3n’+d” を無限に繰り返すことになる。
[論理C’]と[論理D’]を無限に繰り返すと、いずれはn’そのものが2のべき乗に収束する。
このため、[論理E’]は証明できる。
また、数値の基準点をずらしただけの[元]は、[論理B]のビットパターンが変わらないことと合わせて[論理E]も証明できる 。
[KAI要点4]
STEP:22で、2のべき乗に最初に到達する。
このとき、”1″を含めて19桁であり”1″と”0″が18個なので、到達点は218である。
n’が2のべき乗に到達した後も、n’もdも2のべき乗を保ったまま増加し続ける。
[元]が”1″に到達した後、”1→4→2→1→…”の無限ループになる理由がこれである。
[KAI要点5]
仮に”3n’+d”ではなく、”3n’+1″であったとき、n’が218に到達するにはもっとSTEP数は多くなる。
しかし、“+d”は2のべき乗であり、到達点の218に対してSTEP:22と比較的少ないSTEP数でn’が2のべき乗に到達する理由がこれである。
[KAI]は[元]を”d”の”0“の個数分左にずらしただけなので、[からくり2]と合わせて、[元]が比較的少ないSTEP数で”1″に到達する理由もこれである。
以上から、[元]の結論と追加のからくりをまとめると次になる。
[結論1] [論理B]により「n/2が”右に1ビットシフト”である」こと、および「数値の要素となる”1″を含んだビットパターンは変わらない」こと、[論理E]の「nそのものが2のべき乗に収束する」ことから、無限に存在するすべての正の整数は”1″に到達する。
[からくり4] “+1″の数値の基準点が開始時のときより左にずれているため、比較的少ないSTEP数で”1″に到達する。
[KAI]の問題点
数値の基準点がずれないように開始時(STEP:0)のnの数値の基準点=20の桁に固定したため、 n’ とdは値が増加しかしない。
補足に、[元]に”27″を入力したときの例を掲載するが、10進数で見るとSTEP:111、2進数で見るとSTEP:107で、収束した2のべき乗は270である。
これを[KAI]で実現しようとすると、70ビット以上の計算リソースが必要である。
[KAI]の下位のビットにある3倍しても結果”0“にしかならないものを、[元]はうまく計算リソースから除外している。
その副作用で、nの値が増加と減少してしまい、コラッツ予想の式を直感的に理解しずらいものにしてしまっている。
無限ループについて
[KAI]に”1″を入力したときの例を次に示す。
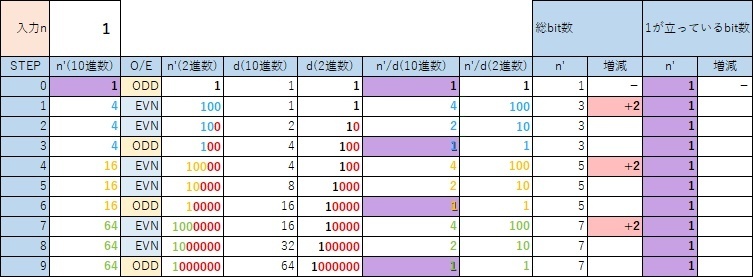
[元]のnは”1″に到達した後、”1→4→2→1→4→2→1→4→2→1→…”の無限ループになるが、その実体のn’は別の値であり、nが偶数時の”n/2″つまり“右に1ビットシフト”により加工された後、見た目が同じ値になっているだけで、[KAI]により見える実体はループしていない。
数値には色が無いので、ループしているように見えているだけである。
[結論1]の「無限に存在するすべての正の整数は”1″に到達する」ことと合わせて、他の値で無限ループすることは無い。
[結論2] “1→4→2→1→…”の無限ループは、偶数時の”n/2″により同じ値に見えるだけで、その実体は無限ループしているわけではなく、また他の値で無限ループすることも無い。
まとめ
からくり
[からくり4]が分かったので、追加して置く。
コラッツ数列に、[論理A~E]を当てはめ、コラッツ予想[KAI]を用いることで、次のからくりが得られた。
- [からくり1]nが偶数になる毎に発生する”右に1ビットシフト”により、数値の基準点となる最下位ビット(20の桁)がSTEP:0(開始時)のn の最下位ビットから左にずれる
- [からくり2]数値の基準点が左にずれるため、”+1″する位置も同様にずれる
- [からくり3]10進数で見た時はn=”1″に到達した時点を”STEP数”としているが、2進数で見た時は2のべき乗となったときを到達点と判断でき”STEP数”に違いがある
- [からくり4]”+1″の数値の基準点が開始時のときより左にずれているため、比較的少ないSTEP数で”1″に到達する。
[からくり1]と[からくり2]が、コラッツ予想を直感的に理解することを難しくしている理由である。
[からくり3]は命題ではないので追及はしない
結論
[からくり1]と[からくり2]の対策により以下の結論を得た。
- [結論1] [論理B]により「n/2が”右に1ビットシフト”である」こと、および「数値の要素となる”1″を含んだビットパターンは変わらない」こと、[論理E]の「nそのものが2のべき乗に収束する」ことから、無限に存在するすべての正の整数は”1″に到達する。
- [結論2] “1→4→2→1→…”の無限ループは、偶数時の”n/2″により同じ値に見えるだけで、その実体は無限ループしているわけではなく、また他の値で無限ループすることも無い。
コラッツ予想の証明の真偽
コラッツ予想「すべてのどの正の整数nで開始しても、最終的に1に到達する(正確には1→4→2→1→…と無限ループになる)と言う予想」は、[結論1]から正しいと考える。
また、[結論2]から他の値で無限ループすることもない。
このため、「コラッツ予想」は予想通り「真」であることを証明できたと考える。
最後に
コラッツ予想をプログラマーが検証してみた では全然説明できていませんでしたが、今回、出来るだけ徹底的に解説したつもりです。
解明には、プログラマー(正確にはソフトウェアアーキテクト)的な発想のものを利用しています。
論理の飛躍や矛盾は無いつもりですが、まだまだ説明不足な部分はあるかと思います。
しかし、コラッツ予想のからくりは理解できるのではなでしょうか?
「徹底解説 コラッツ予想のからくり」の一連の投稿に対して、賛否のご意見、投稿内容の間違い、ご要望などありましたら、ハッシュタグ「#コラッツ予想のからくり #プログラミングの深淵を求めて」を付けてツイートしてください。
また、当サイトでは、今後も私の技術を少しずつ投稿していきます。
是非、Twitter @dratech2020 のフォローをお願いいたします。
なお、コラッツ予想をプログラマーが検証してみた では数式を(改)と表記していました。
今回、数式の記述を見直したこともあり、[KAI]の表記に変更しました。
知的財産権について
本サイトは、本投稿記事の公開時点で、すべて無料で”参照”することが可能です。
ただし、知的財産権(著作権など)を放棄しているわけではありません。
本サイトは、free(無料)で参照できますが、not freedom(自由では無い)です。
個別のテクニックや論理に対しては知的財産権を主張しませんが、それらを組み合わせたものには知的財産権を主張いたします。
©2021 プログラミングの深淵を求めて
https://www.seekabypro.com/
©2021 どらテク(どらぐ~んテクノロジー)
Twitter:@dratech2020 https://twitter.com/dratech2020
関連情報
コラッツ予想の式
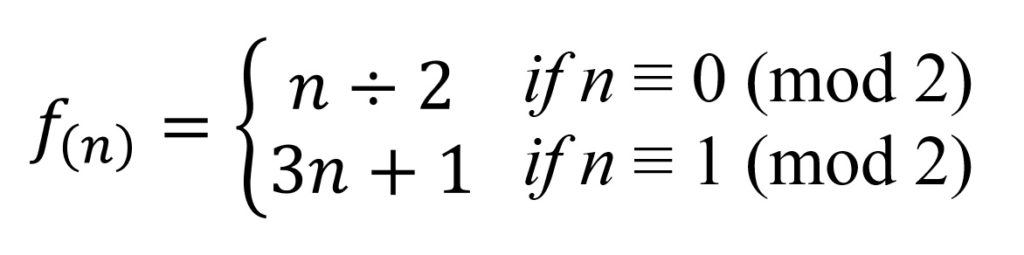
“2”より”3″が大きいのに、すべての正の整数のどの値で開始しても、nは増加傾向にならず、減少して”1″に到達する(その後”1→4→2→1→…”の無限ループになる)という予想。
このように矛盾した結果にたどり着くのは、何故なのか?
関連投稿
徹底解説 コラッツ予想のからくり
これらの投稿は下記の「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。
#1 特徴&論理編
#2 からくり編
#3 結論&証明編(本投稿)
コラッツ予想のからくりのまとめ (2021/12/20追記)
コラッツ予想をプログラマーが検証してみた
#1 要件を確認する
#2 Excelで作ってみた
#3 さらに角度を変えて検証したら・・・!!!
#4 最後に
補足
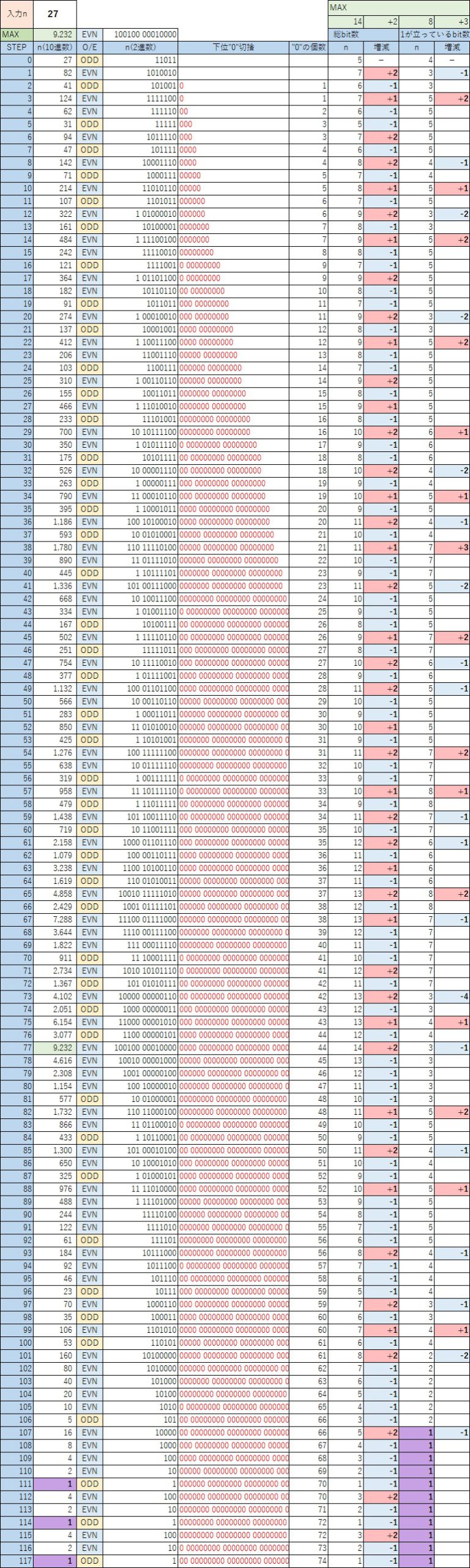
元のコラッツ予想の式で、”27″で 開始したときのコラッツ数列
※[下位”0″切捨]列は、”0″が多くなるため幅を絞っています。





コメント