コラッツ予想のからくり Extra Stage #1 「1→4→2→1→…のループ」がすべてを飲み込む!?

コラッツ数列は1に到達した後、1→4→2→1→…とループになりますがこれに焦点を当てたアプローチ方法です。
2進数で見ると理解しやすい部分は変わりませんが、今までに公開しているものとはまた違ったものになります。
本件は徹底解説 コラッツ予想のからくりやコラッツ予想をプログラマーが検証してみたの説明では不採用としたものですが、特徴的な図を用いたものなので「しくじり先生」的に公開することにしました。

本記事に関連する新しい投稿があります(2023/07/05追記)

はじめに

関連投稿 の記事は、論理的な話が中心でしたが、今回はもう少しビジュアル的なアプローチになっていると思います。
もちろん「コラッツ予想」そのものは変わらないので別の角度から見たものとなります。

「1→4→2→1→…のループ」がすべてを飲み込む!?

徹底解説 コラッツ予想のからくり #1 特徴&論理編 でコラッツ予想の式は“2進数”との親和性が高いことを示したが、この特徴はそのまま利用し、以下のようにコラッツ数列を見ると気が付くことがある。

「70,368,744,177,665」で開始したときの例

コラッツ予想をプログラマーが検証してみた #2 Excelで作ってみた で、Excel版の48bit精度で扱える範囲の中で上位bitと下位bitの”1″で間が最も離れたもの、
10進数で「70,368,744,177,665」2進数で「1000000 00000000 00000000 00000000 00000000 00000001」(“1″と”1″の間に”0″が45個)のコラッツ数列を示した。

この数列のn(2進数bit表示)の下位の部分を見ると気が付くことがある。

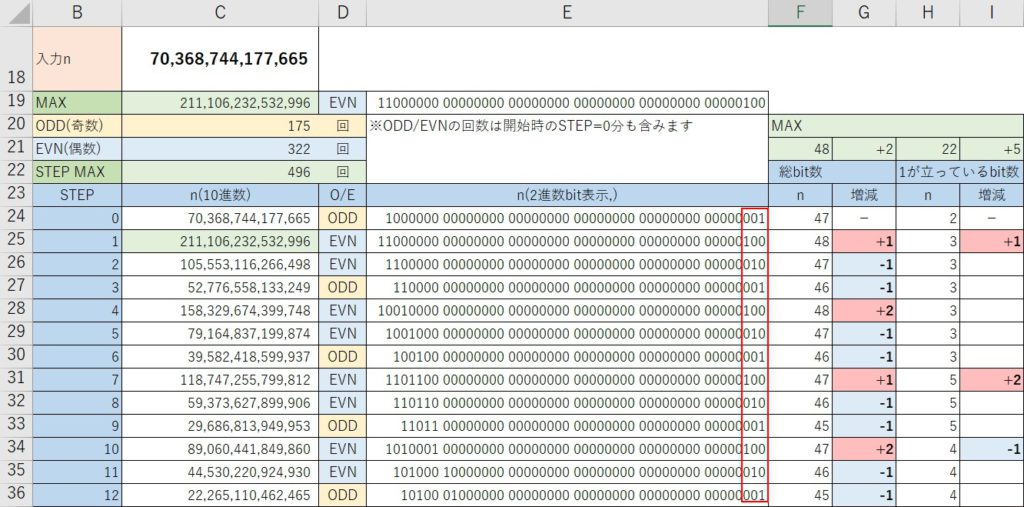
2進数で見た時の下位3bit(赤枠部分)を見ると「001→100→010→001→…のループ」があることに気が付く。
これは、10進数では「1→4→2→1→…のループ」であり、”nが1に到達する前でもその内部では「1→4→2→1→…のループ」が存在する“ことが確認できる。

もちろんこれは、上位bitと下位bitの”1″が最も離れたものであるので、「1→4→2→1→…のループ」が際立って見えると言うのはある。
では、その他の値を含めて検討してみる。

3bit+αの遷移図

関連投稿 でもコラッツの式に対して既に以下のことを述べている。

• nが偶数か奇数なのかは、最下位の1bitのみで判断できること。
• 奇数時の「3n+1」の「3n」はnのすべての桁を3倍にするが、「+1」は最下位の1bitから作用し、桁上がりでしか上位の桁(右側のbit)に作用しないこと。

これらと上記の”nが1に到達する前でもその内部では「1→4→2→1→…のループ」が存在すること”と合わせると、下位の3bitに注目するとよさそうであることがわかる。
これを遷移図にしたものが次である。

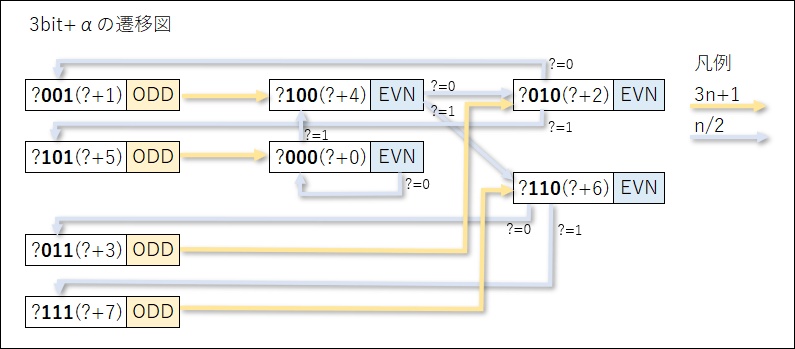
下位3bitより1つ上位のbitは”0″と”1″のどちらもあり得るので”+α“分として図では”?”を用いて記述している。

左上の[?001(?+1)|ODD]は、2進数が「?001」で10進数が「?+1」で「ODD」=奇数であることを表しており、凡例の「3n+1」の黄色の矢印で遷移する。

遷移先の[?100(?+4)|EVN]も同様に、2進数が「?100」で10進数が「?+4」で「EVN」=偶数であることを表しており、凡例の「n/2」の水色の矢印で遷移する。
ただし、”?100″は”?=0″と”?=1″の2つあるので、水色の矢印の遷移も2つある。

これらの矢印の遷移の1回が、コラッツ数列の1ステップに対応します。

他の値についても同様に矢印で繋げていくと上記の図となります。

すべての正の整数の下位3bitは”000″～”111″(10進数で0～7)の8種類しか存在しないため、この遷移図から外れる数値は存在せず、これ以外の遷移も存在しません。

“000”は正の整数ではないので、代わりに”1000″(10進数で8)を用いますが、”001″～”1000″(10進数で1～8)のどれで開始しても、8種類すべて”001″に到達した後、「”001″→”100″→”010″→”001″→…の無限ループ」に収束する(図の最上段)ことはご存じの通り。

このことから下位3bit以外の上位のbitは何であろうと気にする必要はないことを表しています。
また「すべての正の整数で開始しても”1″に到達する(その後1→4→2→1→…の無限ループになる)」こと、また「1→4→2→1→…のループ」以外のループに収束することは無いことを表しています。

つまり、”「1→4→2→1→…のループ」がすべてを飲み込む“と、言いたいのですが、これだけでは説明不足だと感じました。

ブラウザ(BigInt)版 で私が試した最大値“9が1,000個並んだ数値(約2の3300乗)”で開始した例では、最初に”n=1″に到達したSTEP数は 30,578 となります。
これは図の遷移(矢印の移動)が、30,578回発生することを表しており、目視で判断できる範囲を超えてます。
“無限”に作業を続けて確認する方式ではダメと言うこと、“無限”を利用するならば何かに収束する方式でなければダメだと言うことを認識したため不採用としました。
しかしながらループのすべては図の範囲内にしかないので公開することとしました。

まとめ

3bit+αの遷移図から”「1→4→2→1→…のループ」がすべてを飲み込む“と言いたいのだが、“無限”に作業を続けて確認する方式ではダメと言うこと、“無限”を利用するならば何かに収束する方式でなければダメだと言うことを認識できました。

最後に

当初、Excel(48bit)版を作って、論理の構築や確認を行いました。
その後 ブラウザ(BigInt)版で”9が1,000個並んだ数値(約2の3300乗)”と言う、もしかすると前人未到の巨大な数値で開始したコラッツ数列ですら、構築した論理の延長線上にあることを確認しました。
しかし、今回は「下位の3bit+αに注目すれば説明できてしまうのでは無いか?」と言う例です。
私はこれを用いてうまく説明することができませんでした。

しかし、今回のものもプログラミングでよく使われるアプローチの一種です。
ソフトウェアプログラムを作る前などに遷移図(状態遷移図)を用いて対象を分析することは必須技術です。
また、分析だけではなく、仕様のレビュー、テスト/検証項目の洗い出しなど活用方法は多岐にわたりますので、参考になれば幸いです。

通常、プログラムの仕様書は、検討の結果、採用されたもののみ記述することが多く、不採用のものはどこかのメモにあるはずだがどこ行った? ってのがよくあります。
今回の投稿記事は、その不採用としたものを公開するものです。

また、今回は「Extra Stage #1」とのことで、もちろん「Extra Stage #2」の公開も予定しています。
私のTwitterアカウント @dratech2020 のフォローをして頂けると公開時に通知が届きますので、是非フォローをお願いします。
また、投稿ツイートの拡散や感想などを頂けると作者のモチベーションが上がりますので下記の方法でよろしくお願いいたします。

ご意見、ご要望、不具合などのご連絡

ご意見、ご要望、不具合などのご連絡は次からお願いします。

• コメント
  本投稿へ下部の コメントを書き込む からご連絡ください。
  コメントは承認方式となっており、当方が承認しないと公開表示されません。
  公開表示を希望されない方はその旨コメントに記述ください。
• Twitter
  ご連絡は @dratech2020 https://twitter.com/dratech2020 の該当ツイートに返信するか、ハッシュタグ「#コラッツ予想のからくり #プログラミングの深淵を求めて」を付けてツイートしてください。 (すぐに気が付かない場合がありますので、ご了承ください)

関連投稿

ツール:Excel版

ツール:ブラウザ(BigInt)版

ブラウザ(BigInt)版

徹底解説 コラッツ予想のからくり

これらの投稿は下記の「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。

#1 特徴&論理編
#2 からくり編
#3 結論&証明編
コラッツ予想のからくりのまとめ

コラッツ予想をプログラマーが検証してみた

#1 要件を確認する
#2 Excelで作ってみた
#3 さらに角度を変えて検証したら・・・!!!
#4 最後に

コラッツ予想のからくり Extra Stage (2022-06-25追記)

#1 「1→4→2→1→…のループ」がすべてを飲み込む!? (本記事)
#2 コラッツ数列は偶数奇数以外に仕分けできる!? (2022-06-25追記)