コラッツ予想は数学の未解決問題の1つであるが、プログラマー視点から検証した結果どうなるのか?
まずは、要件から確認していく。
本記事に関連する新しい投稿があります(2023/07/05追記)
コラッツ予想とは?
コラッツ予想は、コラッツ問題や3n+1問題などと呼ばれることもある、数学の未解決問題の1つとのことだ。
2021年7月7日に多大な懸賞金がかけられた記事が、PCWatch(https://pc.watch.impress.co.jp/docs/news/yajiuma/1336495.html)に掲載されたことで、私は初めてこのコラッツ予想を知ったのだ。
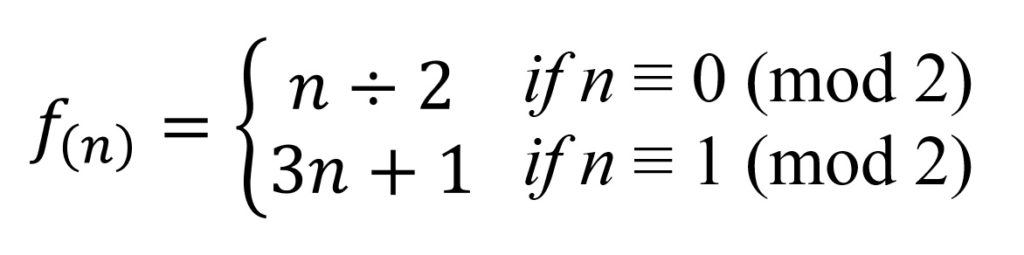
任意の正の整数をnとして入力したとき
- nが偶数の場合は2で割る。その結果を次のnとする。
- nが奇数の場合は3倍して1を足す。その結果を次のnとする。
この計算を繰り返した時、すべてのどの正の整数nで開始しても、最終的に1に到達する(正確には1→4→2→1→4→2→1→…と無限ループになる)と言う予想がある。
私のファーストインプレッションは、偶数と奇数の2種類を扱うため、『「2進数」との相性がよさそうだな、ちょっと挑戦してみようかな?』ぐらいの感覚で検証を始めてみた。
要件を確認する
プログラマーたるもの、要件/要求仕様を確認するのは常である。
要件自体は非常に簡単で、用語の定義と各演算式の入力と出力を理解すれば良い。
- 任意の正の整数
0や小数や分数や負の数を含まない、n=1,2,3,4,5,6,… の数である。 - 偶数
2で割ったときの余り(mod)が0であり、n=2,4,6,… の数である。
nが偶数の時「n÷2」を実施した結果は、1,2,3,…となり奇数の場合と偶数場合がある。 - 奇数
2で割ったときの余り(mod)が1であり、n=1,3,5,… の数である。
nが奇数の時「3n+1」で「3n」を実施した結果は、3,9,15,…と必ず奇数となり、それに「+1」した結果は、4,10,16,…と必ず偶数となる。
フローチャートにしてみる
上記の要件から、フローチャートを作成してみると次となる。
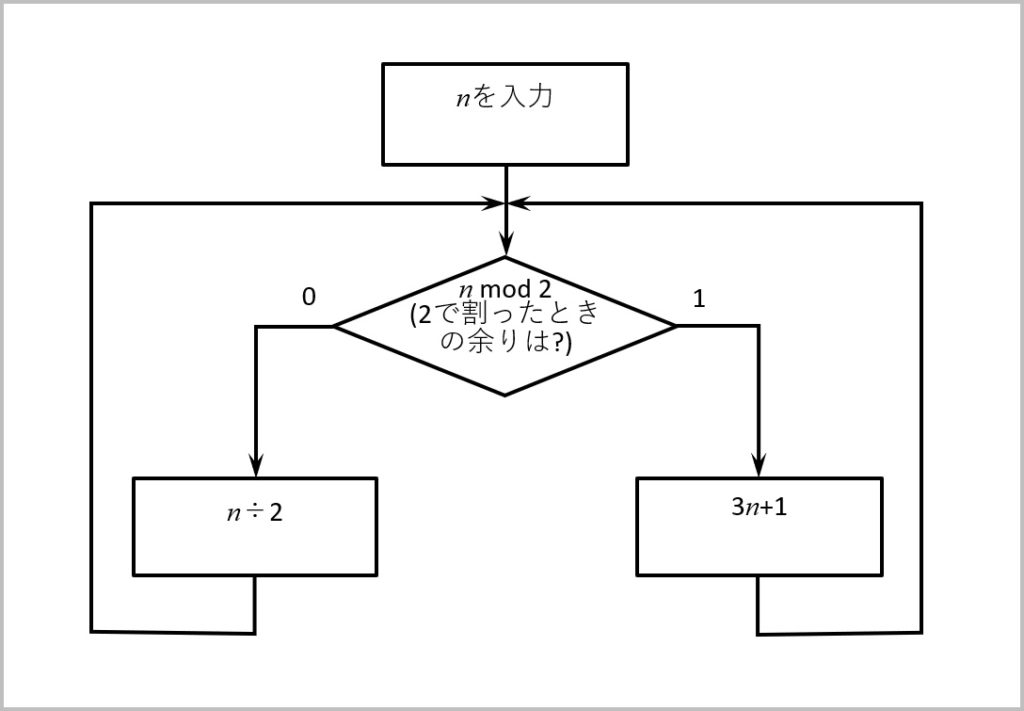
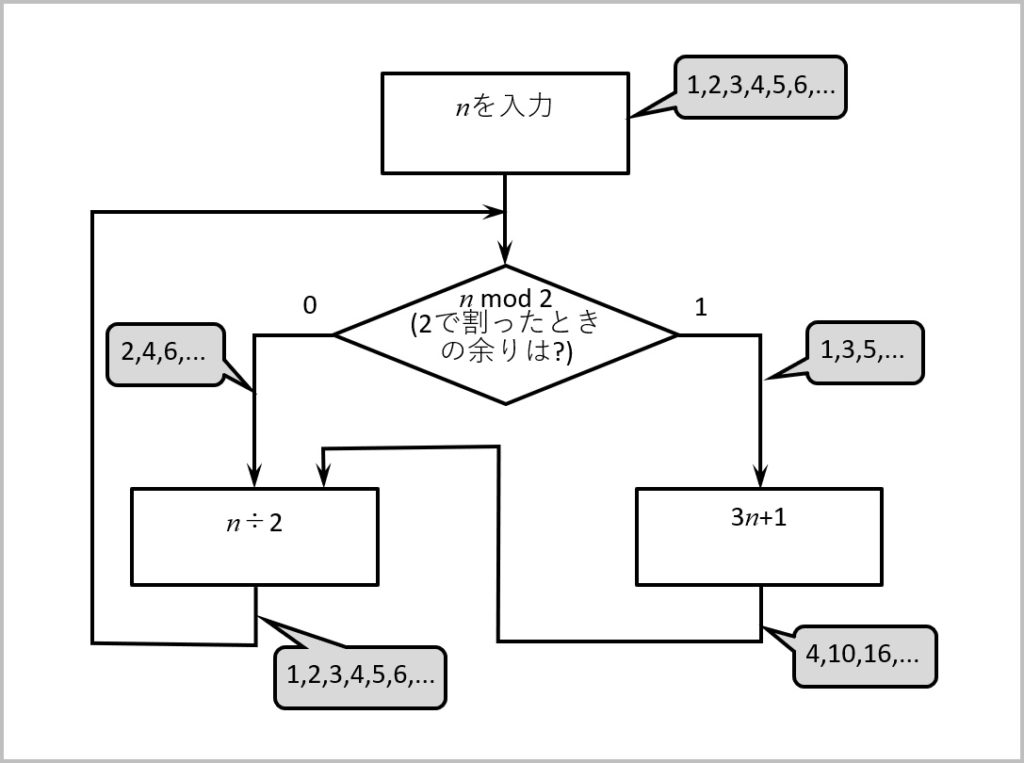
プログラミング的には、上記で正しいのだが、nが奇数のループ(右側のループ)が連続して発生しても良いよう見えてしまう。
nが奇数の時、「3n+1」の結果は必ず偶数なので、下記のように書いた方が人が理解する上では良いかもしれない。
次回に続く
要件を確認したので、次の投稿では、「2進数」を用いて検証してみる。
関連記事
#2 Excelで作ってみた
#3 さらに角度を変えて検証したら・・・!!!
#4 最後に
徹底解説 コラッツ予想のからくり
(2021/11/15追記)
これらの投稿は「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。
#1 特徴&論理編
#2 からくり編
#3 結論&証明編
コラッツ予想のからくりのまとめ (2021/12/20追記)





コメント