コラッツ数列をサクッと確認したいので、Excelで作ってみた。
本記事に関連する新しい投稿があります(2023/07/05追記)
目次
関連情報
Excelファイル
本記事に関連する新しいツールがあります(2023/07/05追記)
下記に出てくる、Excelファイルのリンクをここに置いておきます。
ブラウザ(BigInt)版を公開しました(2021/12/25追記)。
コラッツ予想の式
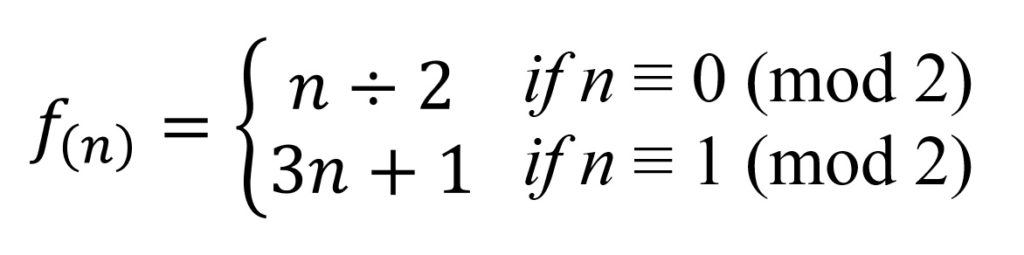
Excelによるコラッツ予想の簡易確認
開発方針
『我々は同じものを見ている。しかし、角度、つまり立ち位置や立場などが違えば、違って見えるはずだ。』と言うことで見る角度を変えてみる。
偶数と奇数の2種類を扱うため、「2進数」との相性がよさそうだが、我々は10進数には馴染みがあるが、2進数にはあまり馴染みが少ない。
実は、スマホやパソコンの内部ではすべて2進数で処理されているのだが、人に見せる部分は10進数など馴染みのあるものに変換して表示してくれている。
コラッツ予想を検証する上でも、何かしらのプログラミング言語で演算結果を出力させるときに、10進数と対応する2進数を表示させたい。
当初は、C++などのコンパイラや、Perlなどのスクリプトで作ろうかと考えていたのだが、これらの出力をどうせExcelなどのスプレッドシートに張り付けて、整形して見やすくするのであれば、最初からExcelで作った方が速いのではないだろうか?
しかも、VBAは利用せず、Excel関数(Excelマクロ)だけで作ることはできないだろうか? ということで、Excelで作ることとした。
Excel関数のみで作ったものを「プログラミング」と呼ぶかは、意見が分かれるところであるが、今回は「コラッツ予想の検証」を目的とするのでこれで良しとする。
2進数について
2進数に馴染みがない方のために、少しここで説明しておく。
なお、知っているよって人は次に進んでも大丈夫です。
我々が一般に使う10進数は、0~9の10種類の数値を使い、0から1ずつ足すと、0,1,2,3,4,5,6,7,8,9となるが、9に1を足すと桁上がりして10となるものであり、同様に99に1を足すと桁上がりして100となるものだ。
一方、2進数は、0と1の2種類の数値を使い、同様に1ずつ足すと、0,1となるが、1に1を足すと、桁上がりして10となるものであり、同様に11に1を足すと桁上がりして100となるものだ。
10進数で”2″の時、2進数では”10″となり、 10進数で”4″の時、2進数では”100″となるものである。
Excelファイル
コラッツ予想を簡易検証するためのExcelファイルを次にて公開します。
Excel関数を用いた計算式は参照できるので細かい説明はここではしないが、コラッツ予想を実現するだけであれば次の図のようにすればよい(10進数のみ)。
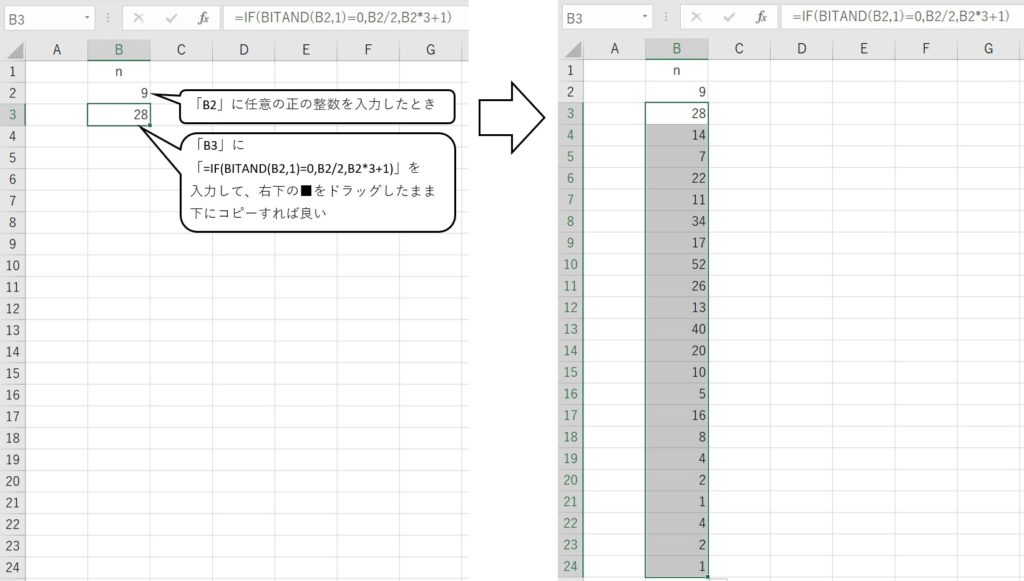
その他、2点ほどExcel関数の制限を回避しているので、その部分のみ解説しておく。
- DEC2BIN関数
10進数(DEC)を2進数(BIN)に変換する関数なのだが、10進数0~511、つまり2進数9桁(9bit)までしか変換ができない。
この回避方法として元の値nを2進数8桁(8bit)ずつに分割してそれぞれ2進数の文字列を作成し、連結することにより、実現している。
なお、Excelの数値の有効桁数が10進数で15桁(2進数で49~50桁あたり)のため、2進数は48桁(48bit)まで実装している。
(2023/10/23追記)
DEC2BIN関数は古い関数で、BASE関数と言う新しい関数があります。
Excelの制限で有効桁数は15桁ですがその最大値999,999,999,999,999をBASE関数を利用することにより2進数文字列に変換することが可能です。
なお、ツールへの適用は2023/10/23現在行っていません。 - MOD関数
割り算の時の「余り」を求める関数なのだが、Excelの数値の有効桁数が10進数で15桁(2進数で49~50桁あたり)なのに対し、MOD関数は2進数で42桁あたりで、「#NUM!」のエラーとなってしまいそれ以上の数値の余りが求められない。
この回避方法として、2種類を使い分けている。- 偶数か奇数かの判定
nを偶数か奇数か判断するときにMOD関数を使って2で割ったときの余りを求めようとすると、2進数で42桁を超える数値で正しく判定できなくなる。
そもそも、偶数か奇数かを見分けるには、10進数では下1桁が、0,2,4,6,8の時が偶数、1,3,5,7,9の時が奇数であるが、2進数では下1桁が0の時が偶数、1の時が奇数である。
このため、BITAND(ビット毎の論理積を求める)関数を用いて、2進数の下1桁の値のみを取得して偶数(=0)か奇数(=1)かを判定することで、MOD関数の制限を回避している。 - その他の余りの取得
元の値をn、これを3で割ったときの余りを求める場合は「n-INT(n/3)*3」のようにする。
なお、INT関数は、整数化の関数で小数点以下を切り捨てるものであり、切り捨てが発生した場合に3倍すると、元のnと切り捨てた分の差分がでるため、これが余りとなる。
- 偶数か奇数かの判定
Excelファイル「collatz-conjecture.xlsx」の[コラッツ予想-48bit]シートの「入力n」に「11」を入力したときの表示例を以下に示す。
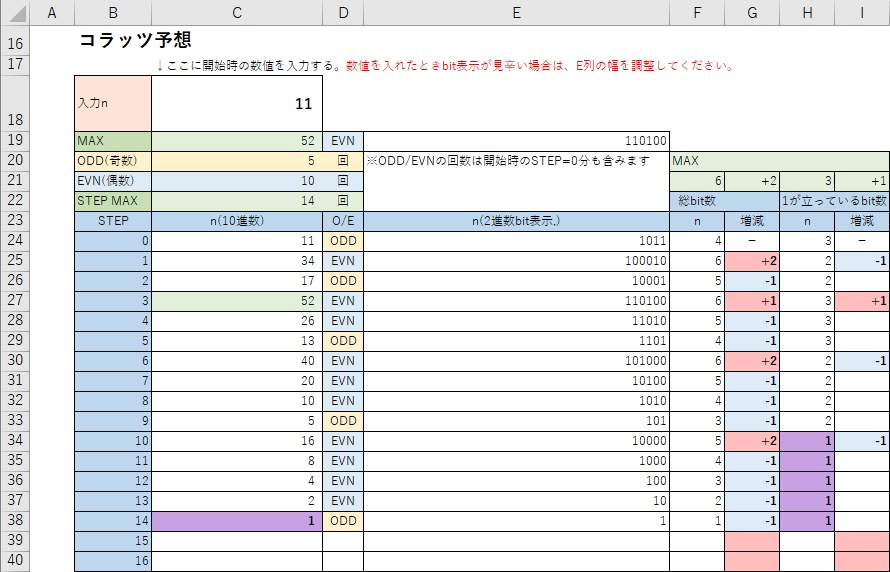
MAX(数列の最大値:薄緑の背景)、ODD(奇数)の回数、EVN(偶数)の回数、STEP MAX(nが1に到達したときのステップ数)、各数値の奇数(黄色の背景)/偶数(水色の背景)、nの2進数(bit表示)、nのbit(桁)数やその増減、1が立っているbit数とその増減を表示している。
また、「入力n」に「27」を入力したときの表示例を以下に示す。
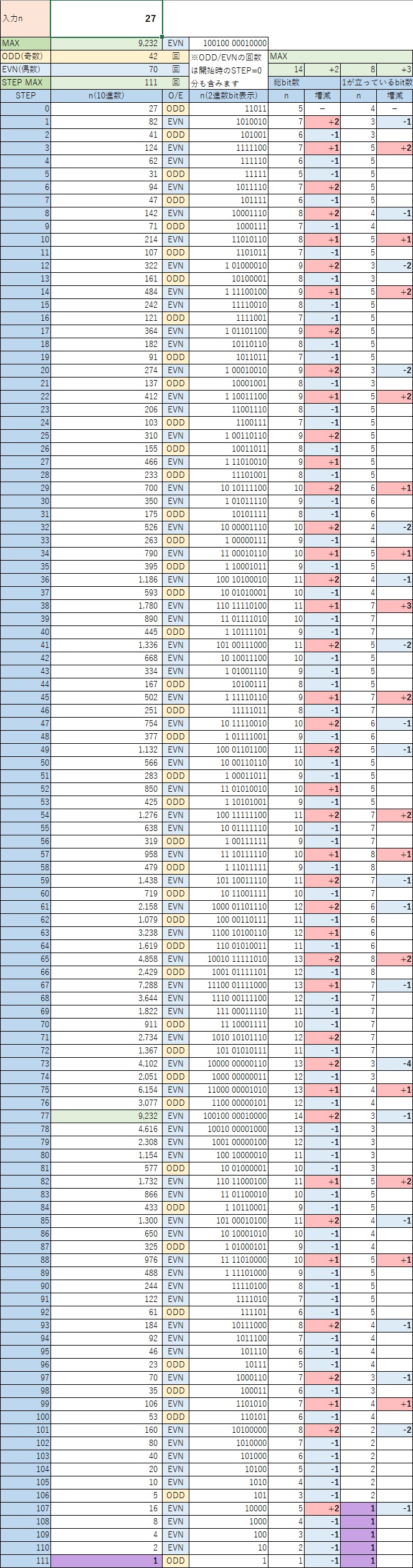
ゴールについて
この [コラッツ予想-48bit]シート では、n(10進数)が1に到達した時点でゴール(紫色の背景)としているが、2進数を見た時、2のべき乗(“27″を入力したときの図のSTEP107~111)となったとき、つまり「1が立っているbit数」が1つのとき(背景が紫色)になると、ゴールに直行していることが分かる。
これは、より大きい32(2の5乗)や64(2の6乗)・・・でも同様にゴールに直行することから、「2進数で見たとき、立っているbitが1つになる(=2のべき乗)と1に到達するのと同等と判断してよい」ことが分かる。
検証
nが偶数の時のn/2について
n/2は、nから2が何回引けるか?を表したものであり、nが偶数である場合は、余りが出ることはない。
今回のExcelの計算式では「n/2」をそのまま利用しているが、昔のコンピューターの内部処理は、この「nから2が何回引けるか?」を割と真面目に実装していたりして、処理速度が遅かった。
当時はまだコンパイラなどの最適化も不十分だったので、高速化するテクニックとして、2などの2のべき乗(2,4,8,16・・・)で割るときは、右にビットシフト(n/2の場合は1ビット分右にシフト,n/4だと2ビット,n/8だと3ビット,n/16だと4ビット・・・)を利用することで、手動最適化していた。
右ビットシフトは、見ただけで結果が推測できるほど簡単なので、コンピューターの処理も速く計算ができる。
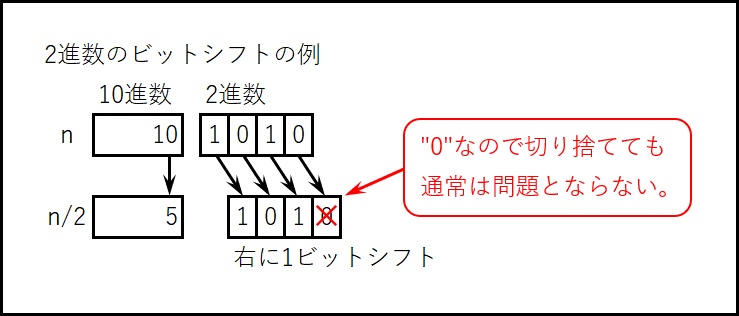
nを右に1ビットシフトしたとき、最下位bitの”0″が切り捨てられるが、nが偶数の場合の最下位bitは常に”0″なので通常切り捨てても問題とならない。
nが奇数の時の3n+1について
いくつか、値を入力してみて、分かったことを以下にまとめる。
- nが2進数で「101(10進数で5)」や「10101(10進数で21)」のように、”1″が1つの”0″と区切られたとき、3n+1は「10000(10進数で16)」や「1000000(10進数で64)」となり、次のSTEPはEVN(偶数,右に1ビットシフト)が続き、1に到達する。
- nが2進数で「1001(10進数で9)」や「100001(10進数で33)」のように、”1″が2つ以上の”0″と区切られたとき、STEP数が比較的多くなる傾向がある。
これらから、「2進数で見た時、上位桁(bit)の1と下位桁(bit)の1ができるだけ離れていればその傾向が見えてくるのではないか?」と考え、以下を検証してみた。
33の例
入力nに「33」を入力したときの例を次の図に示す。
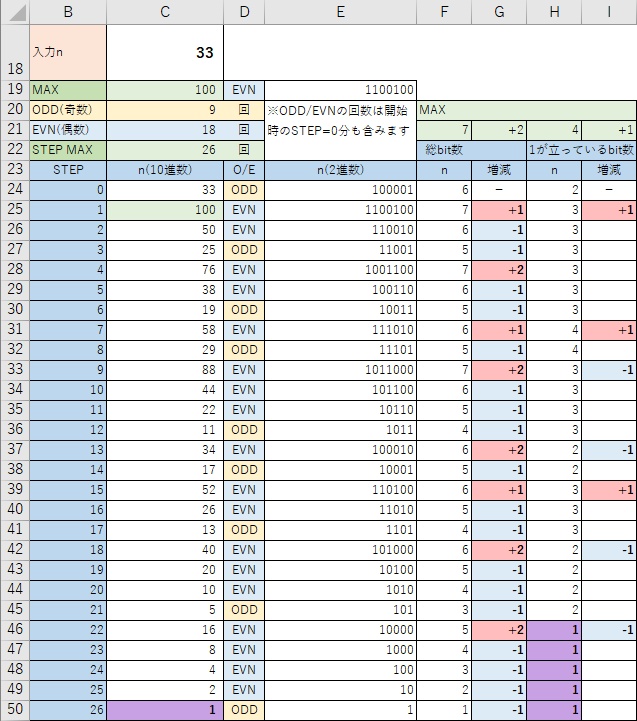
STEP0→1となる部分を少し詳しく見てみる。
| 10進数 | 2進数 | |
| n | 33 | 100001 |
| 3n | 99 | 1100011 |
| 3n+1 | 100 | 1100100 |
3nは、nの左(上位)から右(下位)までのすべての桁(10進数でも2進数でも)を3倍にする(‘0’の部分は3倍しても結果”0″になるだけ)が、+1すると、右の桁に対して作用し始め、桁上がりがあって初めて左の桁に作用する。
10進数で見た時、3nが”99″なので、+1すると桁上がりが発生して”100″となる。
しかし、2進数で見た時、3nは”1100011“であり、+1して桁上がりが発生しても左端の桁まで影響せず”1100100“と、右側(下位)の桁の方が左側の桁より増加が多いことが分かる。
しかも、nが奇数である限り3n+1は必ず偶数であり、右側の端の桁(最下位)が”0″になる。
本Excelで扱える1が離れた最大の数値
Excelファイルをダウンロードしたときの[コラッツ予想-48bit]シートで初期設定してある値、10進数で「70,368,744,177,665」2進数で「1000000 00000000 00000000 00000000 00000000 00000001」(“1″と”1″の間に”0″が45個)で検証した結果が次である。
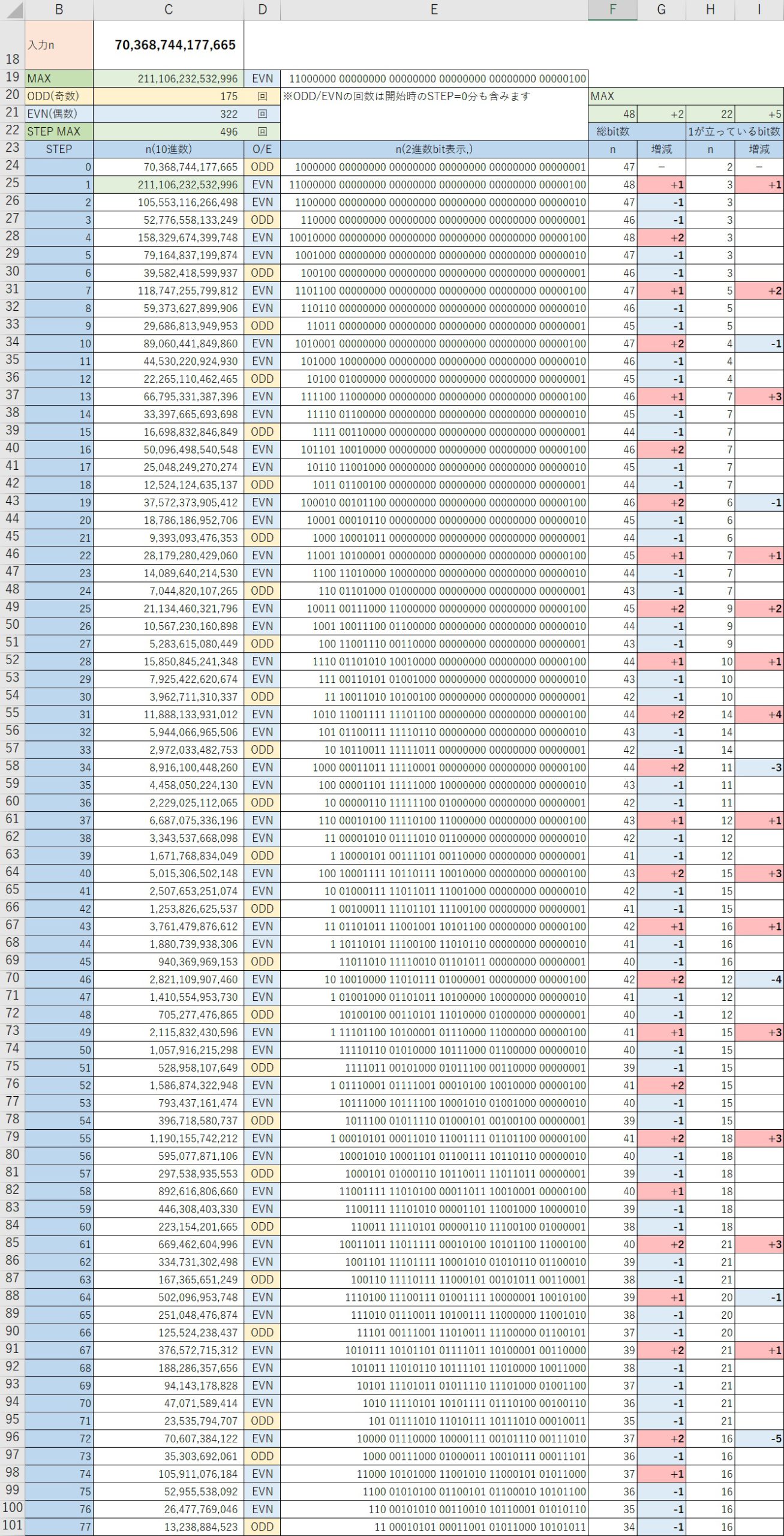
(中略:詳細はExcelファイルで確認してください)
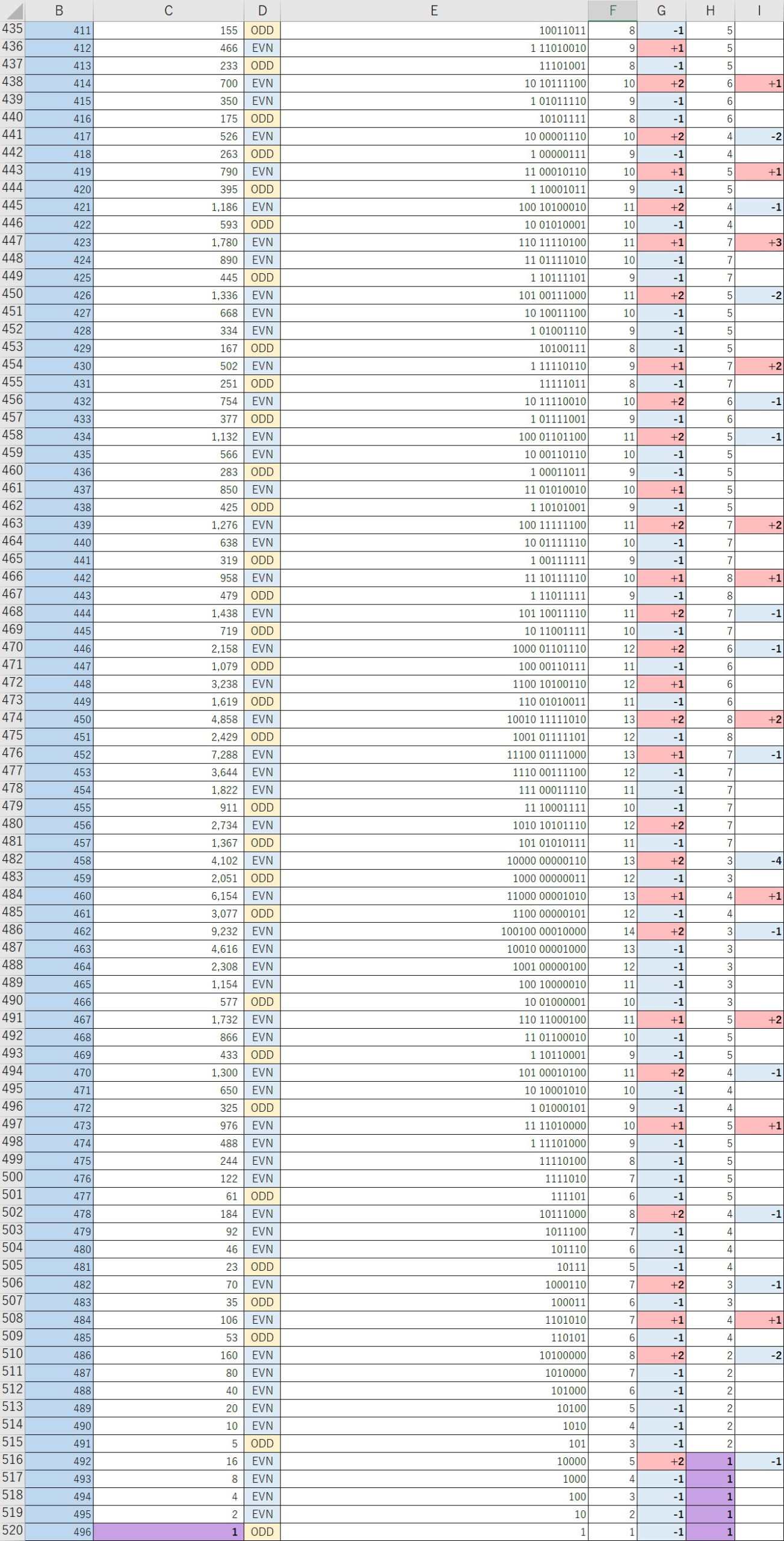
2進数で見た時、”1″と”1″の間に”0″が45個あったとしても+1の分、右(下位)の桁のグループの方が左(上位)の桁のグループより「+1」の分速く増加する。
STEP66,67で侵食が始まり、最終的にSTEP496で”1″に到達する。
また、STEP0~65までの2進数の右から3桁(下位3桁)を見ると、
“1”→”100″→”10″→”1″→”100″→”10″→”1″・・・、
つまり10進数で”1″→”4″→”2″→”1″→”4″→”2″→”1″・・・のループを含んでいることに気付く。
ここまでの検証結果
以上を見て分かるのは、「3n+1で、”nの3倍”は左の桁から右の桁まですべて影響を与えるが、”+1″は右の桁からしか影響を与えない。左の桁に影響を与えるのは桁上がりした時だけ」と言うこと。
これから、「左の桁より、右の桁の方が”+1″の分だけ増加が速い」と言うことが分かる。
また、「nはこの時奇数なので、”3n”も奇数であり、”+1″すると必ず偶数になる」と言うこと。
このため、「増加が速い右側の桁がSTEP数を繰り返すうちに左側の桁を侵食し、それは常に偶数となるため”n/2″、つまり右に1ビットシフトが必ず発生し最終的に1に到達する」と言える。
しかし、これだけでは何か決定打に欠ける。
ここら辺も含め次の投稿で検証する。
関連記事
#1 要件を確認する
#3 さらに角度を変えて検証したら・・・!!!
#4 最後に
徹底解説 コラッツ予想のからくり
(2021/11/15追記)
これらの投稿は「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。
#1 特徴&論理編
#2 からくり編
#3 結論&証明編
コラッツ予想のからくりのまとめ (2021/12/20追記)







コメント
Awesome blog! Do you have any recommendations for aspiring writers?
I’m planning to start my own blog soon but I’m a little
lost on everything. Would you suggest starting with a free
platform like WordPress or go for a paid option? There are
so many choices out there that I’m completely confused ..
Any tips? Appreciate it!
このサイトは AWS Lightsail WordPress インスタンス を利用しています。
Wordpressは無料の範囲内で利用しています。
AWSはもちろん有料です。
私は、独自のプログラムの公開を考えていたため、Wordpressだけでなく仮想マシンから利用することにしました。
バックアップとして仮想マシンのスナップショットを簡単に作れるので便利です。
ただし、サーバー運用に慣れてないと難しいと思います。
This site utilizes an AWS Lightsail WordPress instance.
Wordpress is used within the free range.
AWS is of course charged.
I was thinking of publishing my own program, so I decided to use it not only from WordPress but also from virtual machines.
It is convenient because you can easily take a snapshot of the virtual machine as a backup.
However, I think it will be difficult if you are not accustomed to server operation.