深淵が見えた!!!
ぜひ読んでみてあなたの意見を聞かせてください!!!
本記事に関連する新しい投稿があります(2023/07/05追記)
目次
関連情報
Excelファイル
本記事に関連する新しいツールがあります(2023/07/05追記)
Excelファイルのリンクをここに置いておきます。
ブラウザ(BigInt)版を公開しました(2021/12/15追記)。
コラッツ予想の式
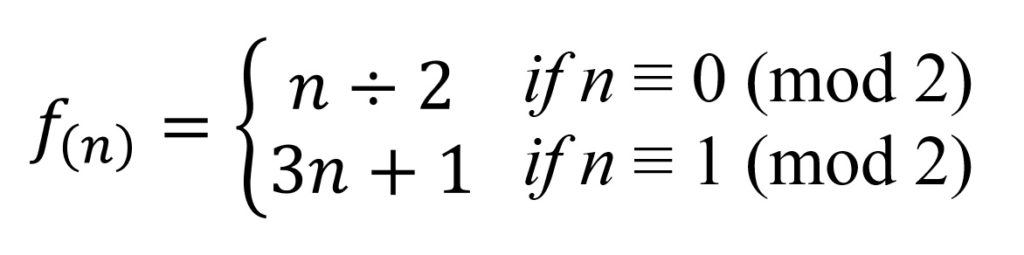
何故、決定打に欠けるのか?
#2 Excelで作ってみた の検証結果から
「増加が速い右側の桁がSTEP数を繰り返すうちに左側の桁を侵食し、それは常に偶数となるため”n/2″、つまり右に1ビットシフトが必ず発生し最終的に1に到達する」のは、何故、決定打に欠けるのだろうか?
コラッツ予想の式を見ると、偶数の時はn/2であるのに対し、奇数の時は3n+1であり、2より3の方が大きいので、値は増加し続けるように見えるのだが、結果は減少し1に到達する。
nは計算を続けると減少と増加が混じっており、それが発生する条件は最初に入力したnに依存するため、減少して1に到達せずに増加するものや、他の値に到達した後それを軸に別のループに陥ってしまうのでないか? と見えてしまう。
『我々は同じものを見ている。しかし、角度、つまり立ち位置や立場などが違えば、違って見えるはずだ。』と言うことで、もう少し2進数で見た時の角度を変えて、増加のみになるようにしてみよう。
アマゾンプライムビデオで「シン・エヴァンゲリオン劇場版」で、見た方も多いのではないかと思うが同時に、独占配信されている「庵野秀明+松本人志 対談」でも出てくるが、『どんな作品でも「角度」で変わる』のだ。
コラッツ予想もいろんな角度から見れば証明に近づけるのではないか?
なお、「庵野秀明+松本人志 対談」に興味がある方は、下記スポンサーリンクから参照ください。
コラッツ予想(改)の提案
- コラッツ予想の奇数時の元の式が「3n+1」であるが、コラッツ予想(改)では「3n+d」とし、dの初期値は1とする。
- コラッツ予想の偶数時の元の式が「n/2」であるが、コラッツ予想(改)では「n」のままで、その代わり「d=d*2」とする。
dは2倍を繰り返すので、値は2のべき乗となり、「2進数で見たとき、”1″が立っている桁(bit)が1つだけ」である。 - コラッツ予想(改)では、偶数と奇数の判定が最下位の桁(右端の桁)では不可能なので、nとdをビット毎の論理積を実施した結果が「0であれば偶数改」、「0より大きければ奇数改」とする。
文章だけではわかりづらいので数式で書くと次のようになるだろうか?
(正しい書き方ではないかもしれないが)
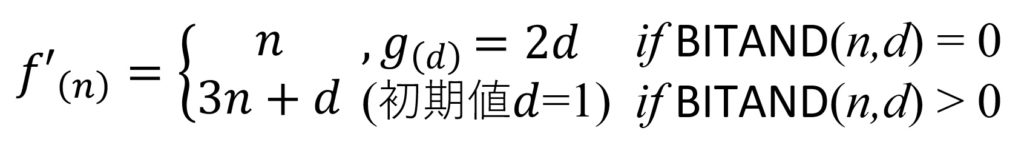
コラッツ予想(改)をExcelで実現するだけであれば次の図のようにすればよい(10進数のみ)。

何故このような式になったのかの説明より前に、Excelファイルの「コラッツ予想(改)-48bit」シートを開放して実際の値を見ながら説明していく。
「コラッツ予想(改)-48bit」シートの開放
Excelファイルにはすでにコラッツ予想(改)の機能を組み込み済みである。
まだダウンロードしてない方は下記から可能です。
(注)すでにダウンロード済みの方は、再度ダウンロードする必要はありません。
次の手順で「コラッツ予想(改)-48bit」シートを開放する。
Excelの下部にあるシートの「タブ(ex.コラッツ予想-48bit)」部分で、右クリックして出てきたメニューで「再表示」をクリックする。
(注)Excel2016でのみ動作確認済み、他のバージョンや別のスプレッドシートでは正しく動作しない場合があります。
表示されたダイアログで
「コラッツ予想(改)-48bit」が選択されていることを確認して[OK]を押せば、シートが表示される。
「コラッツ予想(改)-48bit」で33の例
入力nに「33」を入力したときの例を次の図に示す。
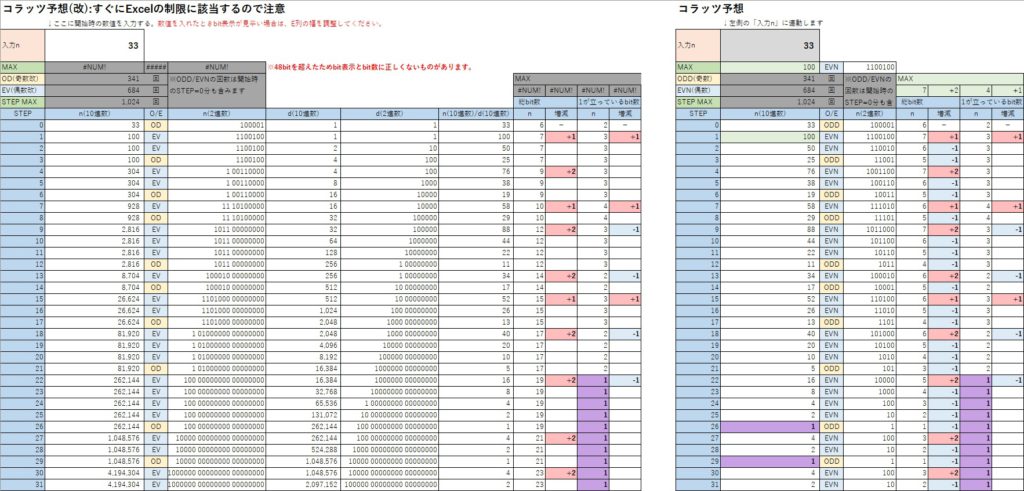
- 左側に「コラッツ予想(改)」を右側に「コラッツ予想」を並べて各STEPを見比べられるようにしてある。
以降の文では、「コラッツ予想(改)」のことを(改)、元の 「コラッツ予想」のことを(元)と略して表記する。 - (元)は、今までのものと少し違い、1に到達しても終了せずに”1″→”4″→”2″→”1″→”4″→”2″→”1″・・・のループを続けるようにしてある。
この関係で、「ODD(奇数)の回数」「EVN(偶数)の回数」「STEP MAX」は意味がないためグレーの背景にしてある。 - (改)のnは増加しかしないため、「MAX」および「OD(奇数改)の回数」「EV(偶数改)の回数」「STEP MAX」は意味がないためグレーの背景にしてある。
- (改)は(元)と比べて「d(10進数)」「d(2進数)」「n(10進数)/d(10進数)」の列が追加してある。
(改)の「n(10進数)/d(10進数)」と(元)の対応するSTEPの「n(10進数)」とが同じであることが分かる。
表では横に長くなるため省略したが、(改)の「n(2進数)/d(2進数)」と(元)の「n(2進数)」も同じになる(同じ値を10進数と2進数の別角度から見ているだけなので違うはずがない)。
このため、「コラッツ予想(改)」は、「コラッツ予想」を別の角度から見たものであることが分かる。
ただし、この「コラッツ予想(改)」のExcel表には問題がある。
値が増加しかしないため、入力するnの値によっては、すぐにExcelで扱える値の限界に達してしまう。
検証する分にはこのままで十分であるが、回避方法はあるので、それは後述する。
コラッツ予想(改)による検証
下記には冗長な情報が出てきます。
そもそも同じものを角度を変えて見ているだけなので、多くは冗長な情報です。
nの値について
(改)の「n(10進数)」の値そのものにはあまり意味は無いが「n(2進数)」は、(元)の「n(2進数)」のビット列をd(2進数)分桁上げしたものである。
上記「33の例」のSTEP3では、(改)の「n(2進数)」は”1100100“で、(元)の「n(2進数)」の”11001“を「d(2進数)」の”100“分桁上げしたものである。
偶数改と奇数改を判定するとき、(改)の「n(2進数)」を「d(2進数) 」で割ると (元)の「n(2進数)」が求められるので、その最下位の桁を見て”0″なら偶数、”1″なら奇数を判断することは可能である。
ex.) BITAND(n/d,1) の結果が”0″なら偶数、”1″なら奇数
しかし、「d(2進数) 」は2のべき乗であり、”1″が立っている桁(ビット)は1つだけである。
このため、わざわざ「n/d」で割り算をする必要はなく、nとdのビット毎の論理積(BITAND(n,d)) で求めた結果が、”0″なら偶数改、”0″より大きいなら奇数改と判別することができる。
コンピューター自体、論理式(AND,OR,NOT)の組み合わせで作られており、四則演算(+-×÷)も論理式の組み合わせで作られている。
当然、割り算を実行するより、論理積(AND)を実行する方が計算リソースとして規模が少なく省電力だし、実行速度も速い。
こういう最適化の方法を知っていれば、今後の総プログラミング時代でも差をつけられると思う。
偶数改と奇数改
(改)の偶数改は「n」をそのまま返すので注視する必要がない。
このため、奇数改である「3n+d」のみ注視すればよい。
奇数改は、n(2進数)とd(2進数)のビット毎の論理積(BITAND)の結果が、0より大きいときである。
d(2進数)は2のべき乗なので、”1″が立っている数は1つだけであり、n(2進数)の同じ位置にも”1″が立っている。

また、「3n」で3倍すると言うことは上位と下位の桁を等しく3倍することであり、「n(2進数)の下位の”0″の部分は3倍した結果”0″となる」だけであり、計算してもしなくても結果は変わらない。
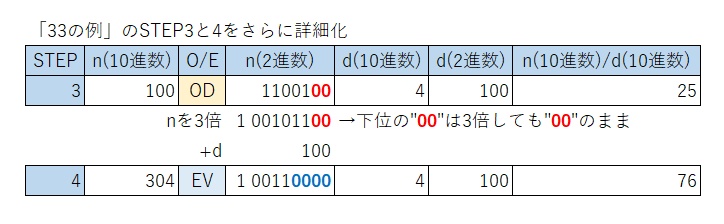
(元)の偶数時の「n/2」は、右に1ビットシフトであり、その都度、2進数で見た時の「3倍した結果”0″となる下位の桁」の部分(上の図の”0000“)を除外して桁数を減らすが、数値を表す”1″が立ったビットパターンは変えないことで、計算リソースを節約している(“100110000“→”10011“)。
その副作用として、nの値の減少と増加が発生してしまい、人が直感的に正しく見ることを難しくしている。
しかし、(改)の振る舞いから分かるように(元)は「増加が速い右側の桁がSTEP数を繰り返すうちに左側の桁を侵食し、それは常に偶数となるため”n/2″、つまり右に1ビットシフトが必ず発生し最終的に1に到達する」ことであることが確認できる。
なお、「3n」の部分は「奇数倍」であれば、「n」や「5n」や「7n」などなんでも良く、入力された値によりSTEP数に違いが出るが、(改)の「+d」および(元)の「+1」による桁上がり(その部分は2のべき乗を含む)が発生し上位(左側)の桁より下位(右側)の桁が速く増加するため、このルールが成り立つ。
コラッツ予想(改)のゴール
(改)のゴールは、「2進数で見たとき、”1″が立っている桁(bit)が1つ(=2のべき乗)になったとき」であるが、その後にnもdも無限に増加し続けるため明確なゴールは無い。
(元)のnが”1″に到達した後、10進数で”1″→”4″→”2″→”1″→”4″→”2″→”1″・・・の無限ループになる理由がこれである。
これは、「無限に存在するすべての正の整数は、上記のルールから外れることはない」ことを表している。
「無限に増加」および「無限ループ」することから分かるように、「+d」および「+1」が無限に発生するため、STEP数の違いはあれ、いずれ「2のべき乗」および「1」に到達すると言う仕組みである。
コラッツ予想(改)のExcelの問題の回避
問題点
コラッツ予想(改)のExcelでの実装の問題として、nおよびdは増加しかしないので、すぐにExcelの扱える値の範囲を超えてしまう(計算リソースが足りない)ことである。
「70,368,744,177,665」を入力したときはもちろん、「27」を入力したときもSTEP数を繰り返すうちに「#NUM!」のエラーとなってしまう。
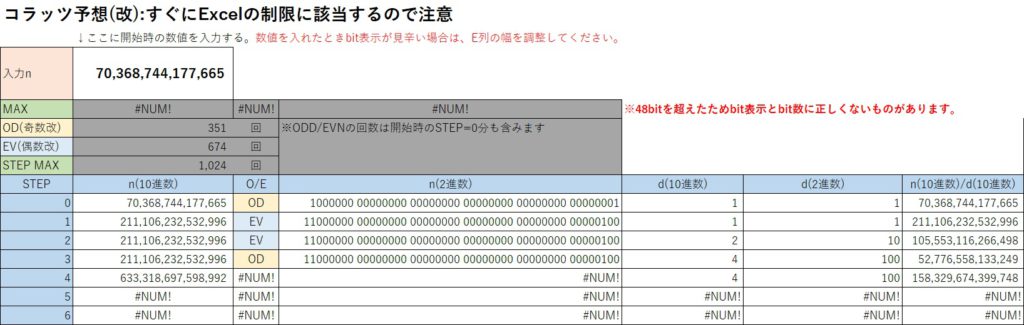
解決方法
どうすれば、解決できるだろうか?
欲しいものは、(改)の「n(2進数)」であり、「n(10進数)」や「d(10進数と2進数の両方)」は無くても良い。
(元)の偶数時の「n/2」は「右に1ビットシフト」であることを何度も言ってきた。
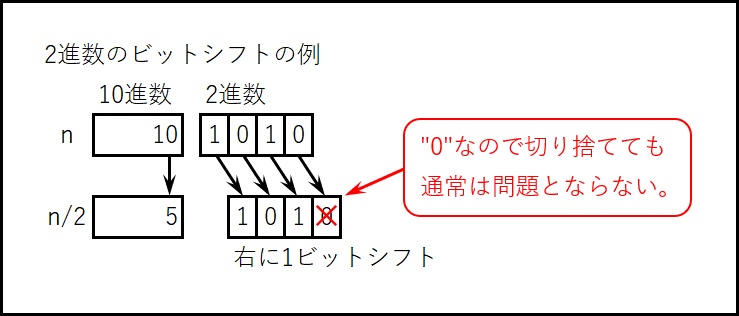
「右に1ビットシフト」時に「最下位の桁の”0″は切り捨てても通常は問題とならない」と言ったが、今回はこれを記録することで解決が可能である。
「下位”0″切捨」の開放
当然ながら、この機能も既にExcelファイルに実装済みである。
以下の手順で開放しよう。
「コラッツ予想(改)-48bit」シートの右側の(元)の「コラッツ予想」の方の「AJ」の上に[+]の表示があるのでこれをクリックする。
(注)Excel2016でのみ動作確認済み、他のバージョンや別のスプレッドシートでは正しく動作しない場合があります。
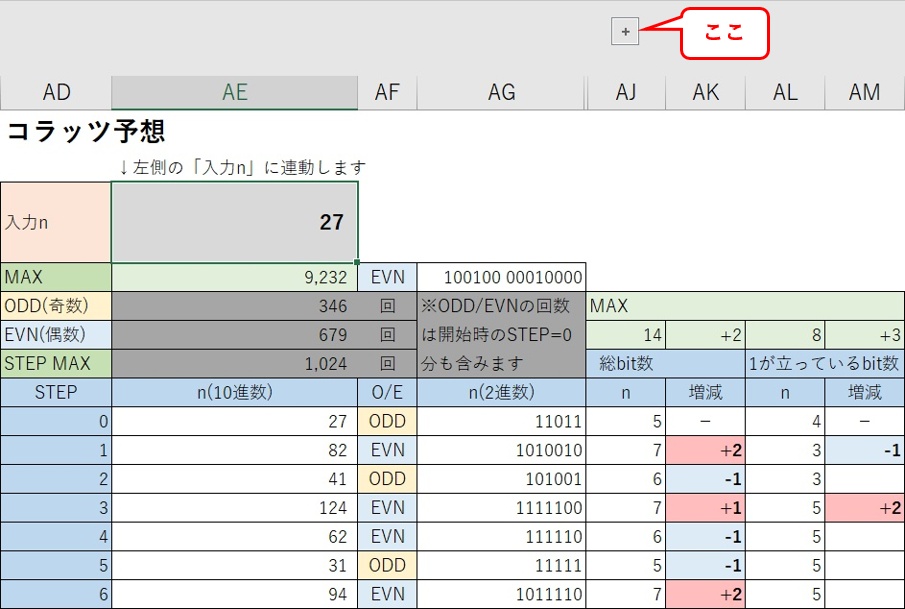
「下位”0″切捨」と「”0″の個数」が表示される。
(元)の「n(2進数)」と「下位”0″切捨」を連結すると(改)の「n(2進数)」と同じとなる。
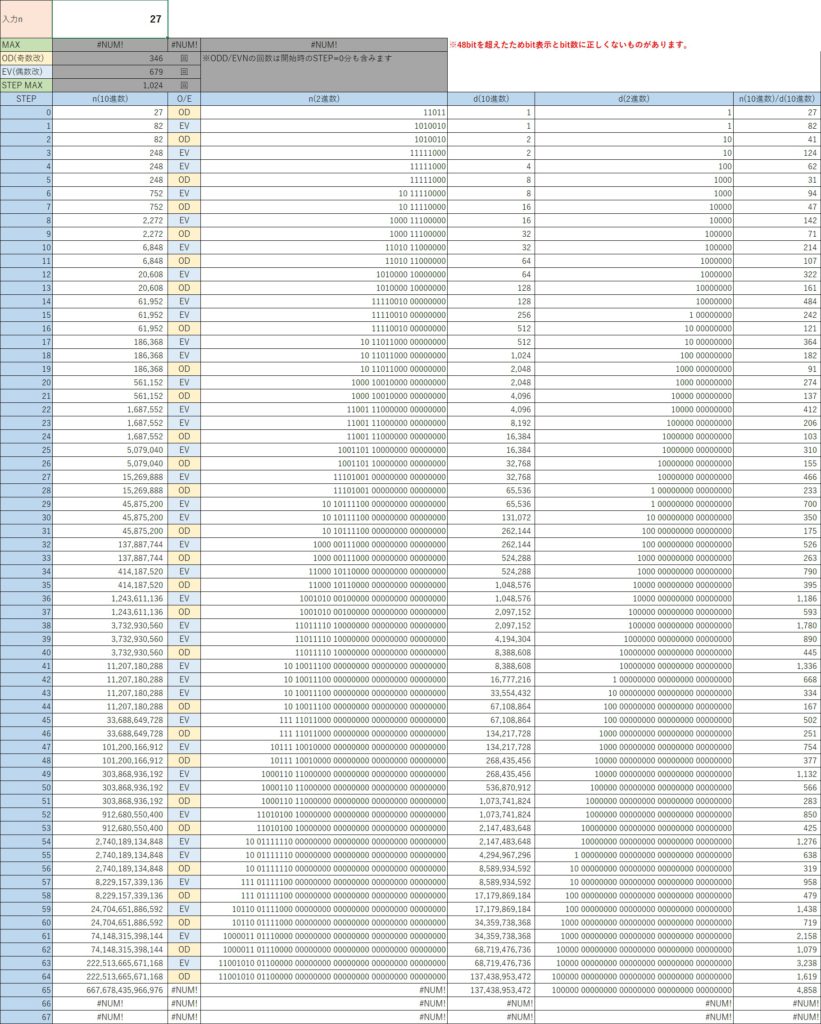
以下に「27」を入力した例を示す。
(「下位”0″切捨」 の列「AH」は横に長くなりすぎるため幅を縮めてます)
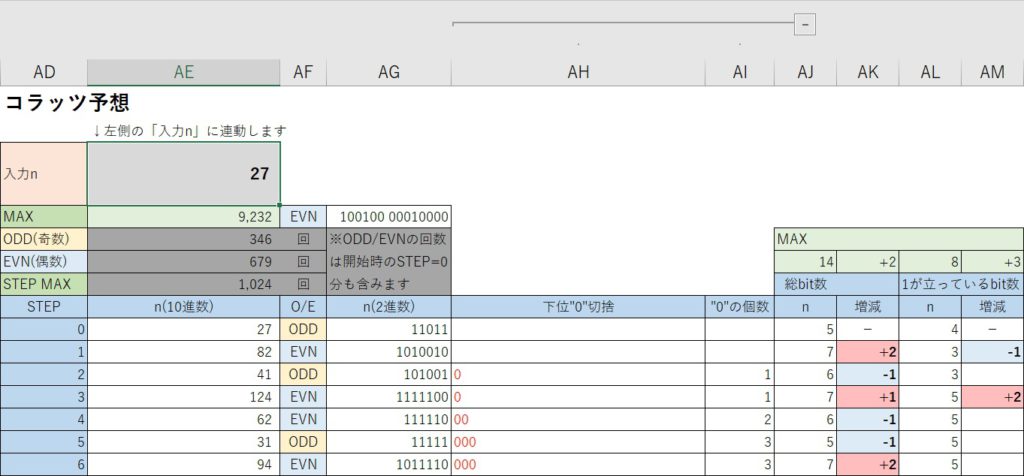
(中略:詳細はExcelファイルで確認してください)
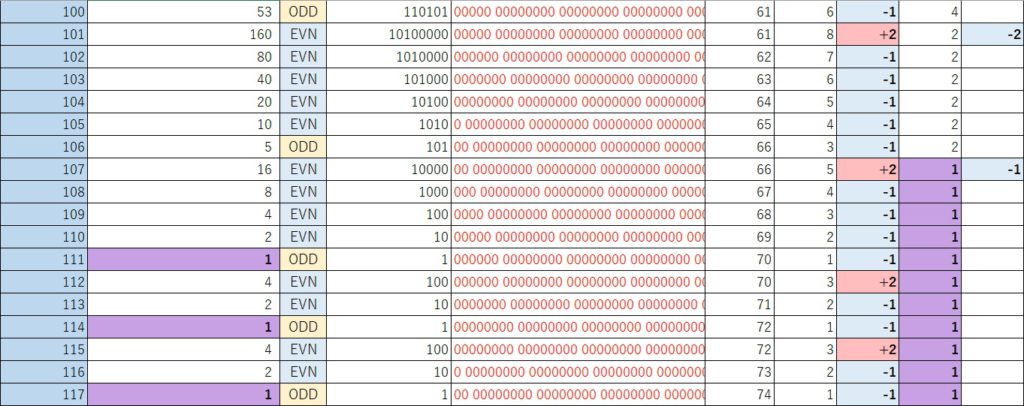
これで、コラッツ予想(改)の「n(2進数)」を48bit精度のままで検証することが可能となる。
「27」を入力した例では、(元)のSTEP111でnが1に到達するが、(改)では、2の70乗(“0″が70個付く:”1″が2の0乗,”10″が2の1乗のため)に到達していることが分かる。
その後、それぞれ、無限ループと無限増加が発生しているが確認できる。
なお、nが偶数の時は右に1ビットシフトであり、1つずつ”0″が切り捨てられるため、「”0″の個数」の最大値は「偶数の出現回数」と同じとなる。
(注) 「下位”0″切捨」と「”0″の個数」は切り捨てられた後に記録するため、表では「EVN」の次の行で+1されます。
まとめ
- コラッツ予想は、2進数(ビット)で見ると理解しやすい。
- 2進数の場合、偶数と奇数は、最下位の桁のみ見ればよく、”0″なら偶数、”1″なら奇数となる。
- 偶数時の「n/2」は、右に1ビットシフトであり、最下位の桁の”0″を除外することになる。
これは計算リソースを節約しているものであり、数値の要素である”1″を含むビットパターンに変化はない。 - 奇数時の「3n+1」の「3n」は、nの上位から下位の桁を等しく3倍するが、「+1」はnの下位の桁からのみ作用し、上位の桁より下位の桁の方が速く増加する。
nが奇数なので「3n」も奇数であり、「+1」すると必ず偶数、つまり下位の桁に2のべき乗(2の0乗=1以外)を含むことになる。
10進数で見ててもダメな理由は、2のべき乗が含まれることに気が付かないことです。
しかし、2進数で見るとすぐに気づけます。 - この偶数時と奇数時の組み合わせのSTEPを繰り返すことで、「3n+1」による増加で必ず下位の桁に2のべき乗を含み、その度に「n/2」、つまり右に1ビットシフトが発生し値が減少する。
- 増加のみ(コラッツ予想(改))に角度を変えた場合の到達値は、右に1ビットシフトで除外した”0″の個数、つまり偶数の発生回数と、最上位の桁の”1″の分を足した桁数分の2のべき乗になる。
- 結果的にその都度発生する右に1ビットシフトによりnは”1″に到達する。
その後、nは10進数で”1″→”4″→”2″→”1″→”4″→”2″→”1″・・・の無限ループになる。
これは、無限に存在するすべての正の整数を入力しても、結果的に”1″に到達することを表している。 - 以上により、コラッツの予想である「すべてのどの正の整数nで開始しても、最終的に1に到達する(正確には1→4→2→1→4→2→1→…と無限ループになる)と言う予想」は真であると証明できたのではないだろうか?
関連記事
#1 要件を確認する
#2 Excelで作ってみた
#4 最後に
徹底解説 コラッツ予想のからくり
(2021/11/15追記)
これらの投稿は「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。
#1 特徴&論理編
#2 からくり編
#3 結論&証明編
コラッツ予想のからくりのまとめ (2021/12/20追記)







コメント